Question

A ladder on the platform of a fire brigade van can be elevated at an angle of $ {70^ \circ } $ to the maximum. The length of the ladder can be extended up to $ 20m $ . If the platform is $ 2m $ above the ground, find the maximum height from the ground up to which the ladder can reach $ \left( {\sin {{70}^ \circ } = 0.94} \right) $ .

Answer 1

Hint: In order to find the maximum height from the ground, make a rough diagram of the information given, an angle of elevation from the height of the fire-brigade and the length of the ladder. Use the trigonometric identity $ \sin \theta = \dfrac{{perpendicular}}{{hypotenuse}} $ , substitute the values known and solve the equation to find the height.
Formula used:
 $ \sin \theta = \dfrac{{perpendicular}}{{hypotenuse}} $

Complete step-by-step answer:
Considering the height from the ground to be DC, Ladder to be AD, and the platform of the fire-brigade to be AD.
It is given that the angle of elevation from the platform to the height is $ {70^ \circ } $ .
The information given in the question above is $ AB = 2m $ , $ AD = 20m $ and $ DC = h $ .

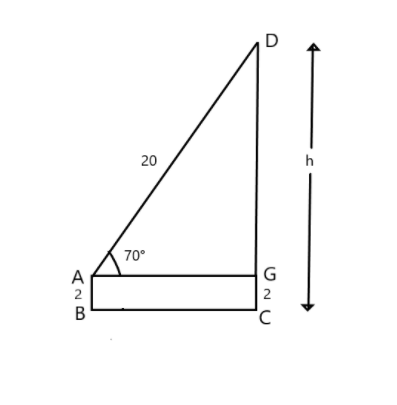
According to the following information, the rough diagram represented is:


From the given figure, it is seen that:
 $ DG = CD - CG $ …….(1)
As we can see that $ AB = CD = 2 $
Substituting the value of $ CD $ and $ CE $ in (1), we get:
 $ DG = \left( {h - 2} \right)m $
From trigonometric identities, we know that:
 $ \sin \theta = \dfrac{{perpendicular}}{{hypotenuse}} $
In right triangle $ \Delta AED $ , substituting the angle of elevation $ \theta = {70^ \circ } $ , perpendicular $ DG = \left( {h - 2} \right)m $ and hypotenuse $ AD = 20m $ in the above equation, we get:
\[\sin {70^ \circ } = \dfrac{{DE}}{{AD}}\]
\[ \Rightarrow \sin {70^ \circ } = \dfrac{{h - 2}}{{20}}\]
Substituting the value of $ \left( {\sin {{70}^ \circ } = 0.94} \right) $ as given in the question:
\[ \Rightarrow 0.94 = \dfrac{{h - 2}}{{20}}\]
Multiplying both the sides by \[20\]:
\[ \Rightarrow 0.94 \times 20 = \dfrac{{h - 2}}{{20}} \times 20\]
\[
   \Rightarrow 0.94 \times 20 = \dfrac{{h - 2}}{{20}} \times 20 \\
   \Rightarrow 18.8 = h - 2 \;
 \]
Adding both the sides by \[2\]:
\[
   \Rightarrow 18.8 + 2 = h - 2 + 2 \\
   \Rightarrow 20.8 = h \\
   \Rightarrow h = 20.8 \;
 \]
Height \[h = 20.8m\].
Therefore, the maximum height from the ground up to which the ladder can reach is \[20.8m\].
So, the correct answer is “\[20.8\;m\]”.

Note: Diagram representation for this type of questions is very important for solving it easily.
The angle of elevation is nothing but the angle formed from the point to the ground to the height above the ground whereas the reverse i.e, the angle from the point above the ground to the point on the ground is called angle of depression.