Question

A ladder is inclined to a wall making an angle of \[30^\circ \] with it. A man is ascending the ladder at the rate of 2 m/s. How fast is he approaching the well ?
A. 2 m/s
B. 1.5 m/s
C. 1 m/s
D. 0.5 m/s

Answer 1

Hint:- Man is ascending the ladder at the rate of 2m/s means that the slant speed is 2m/s. And how fast he is approaching means horizontal speed. Soo, we had to find the horizontal speed if the slant speed was given.

Complete step by step solution:
Let us first draw the diagram so that we can understand the problem easily.

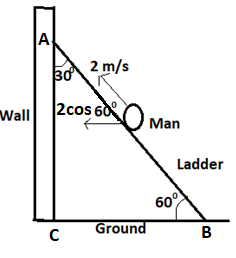
As we can see from the above figure that man is ascending the ladder at a speed of 2m/s or we can say that the speed along line BA is 2m/s.
Now we are asked to find how fast the man is approaching the wall or in other words the speed of man along line BC.
So, as we know that walls and ground are always perpendicular. So, the angle ACB must be equal to \[90^\circ \].
As we know that the sum of all angles of a triangle is equal to \[180^\circ \] and the angle CAB (i.e. angle made by ladder with wall) is given as \[30^\circ \].
So, the angle ABC = \[180^\circ - 90^\circ - 30^\circ = 60^\circ \]
Now as we know that if the slant speed is x then the horizontal speed will be \[x\cos \theta \], where \[\theta \] is the angle made by the base with slant. And vertical speed will be \[x\sin \theta \], where \[\theta \] is the angle made by the perpendicular line with slant.
Hence, the horizontal speed will be equal to \[2\cos 60^\circ \].
Now as we know that \[\cos 60^\circ = \dfrac{1}{2}\].
So, the horizontal speed will be = \[2 \times \dfrac{1}{2} = 1\]m/sec
So, the man is approaching the wall at the speed of 1m/s.
Hence, the correct option will be C.
Note:- Whenever we come up with this type of problem then first, we had to draw the diagram because it makes the problem easier to understand and after that if we know the slant speed (like speed at which man is ascending wall) and asked to find horizontal speed (like how fast man approaching wall) then we can direct use formula horizontal speed = slant speed*\[\left( {\cos \theta } \right)\], where \[\theta \] will be the angle between slant speed and horizontal speed. This will be the easiest and efficient way to find the solution of the problem.