Question

A ladder 5m long is leaning against a wall. The bottom of the ladder is pulled along the ground away from the wall, at the rate of 2m/sec. How fast its height on the wall decreasing when the foot of the ladder is 4m away from the wall.
\[\begin{align}
  & \text{A}.\text{ }\dfrac{4}{3}\text{ m}/\text{sec} \\
 & \text{B}.\text{ }\dfrac{8}{3}\text{ m}/\text{sec} \\
 & \text{C}.\text{ }\dfrac{10}{3}\text{ m}/\text{sec} \\
 & \text{D}.\text{ }\dfrac{6}{3}\text{ m}/\text{sec} \\
\end{align}\]

Answer 1

Hint: First, we will draw the figure and will get a right-angled triangle. Assume height as y, then, by Pythagoras theorem, find the solution between the height of the wall and distance from the wall. Converting the equation in a single variable differentiate the equation with respect to time, because this gives the desired rate at which the height on the wall is changing. Then, substitute x=4m to get the rate of decrease of height.

Complete step by step answer:
A ladder that is 5m long is leaning against a wall and the bottom of the ladder is being pulled, we need to find at which rate the height on the wall is decreasing. We will have a condition like this:

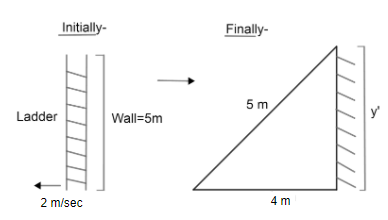
Suppose, the height on the wall is 'y' when the ladder is 4m away from the wall.
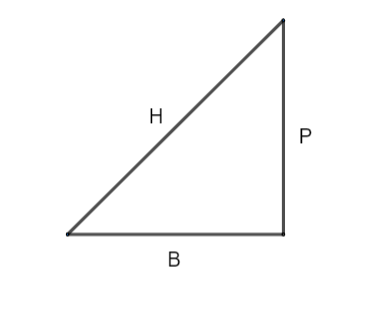
By Pythagoras theorem,
\[{{H}^{2}}={{P}^{2}}+{{B}^{2}}\]

As per the question, at any time ’t’ the figure would be:
\[\begin{align}
  & {{5}^{2}}={{x}^{2}}+{{y}^{2}} \\
 & {{y}^{2}}={{5}^{2}}-{{x}^{2}} \\
 & {{y}^{2}}=25-{{x}^{2}} \\
 & y=\sqrt{25-{{x}^{2}}} \\
\end{align}\]

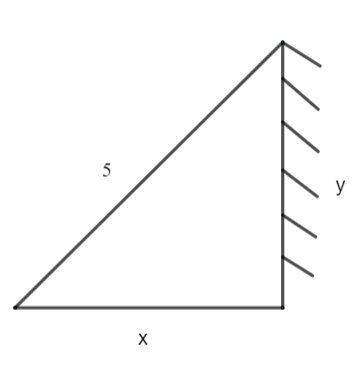
Now, we have the relation of height on the wall y and distance from the wall x in one variable .i.e.
\[y=\sqrt{25-{{x}^{2}}}\]
But, the question is asking about rate of change of height on wall that is \[\dfrac{dy}{dt}\]
Therefore, differentiating 'y' with respect to time ’t’.
\[\begin{align}
  & \dfrac{dy}{dt}=\dfrac{d}{dt}\left( \sqrt{25-{{x}^{2}}} \right) \\
 & \Rightarrow \dfrac{dy}{dt}=\dfrac{-x}{\sqrt{25-{{x}^{2}}}}\times \dfrac{dx}{dt} \\
\end{align}\]
It is given that, rate of change of the distance from wall i.e. \[\dfrac{dx}{dt}\] is 2 m/sec.
\[\Rightarrow \dfrac{dy}{dt}=\dfrac{-2x}{\left( \sqrt{25-{{x}^{2}}} \right)}\]
We need to find the rate of change of height on the wall when the bottom of the ladder is at a distance 4m away from the wall. So, put x=4m.
\[\Rightarrow \dfrac{dy}{dt}=\dfrac{-2\times 4}{\left( \sqrt{25-4\times 4} \right)}=\dfrac{-8}{\sqrt{9}}=\dfrac{-8}{3}\]
Hence, the height of the ladder on the wall is decreasing at the rate of \[\dfrac{8}{3}m/sec\]
Therefore, the correct option is B.
Note:
 Students must be very clear and specific for using Pythagoras theorem at right place because it will convert the two-variable problems into a single one. Students must also be aware of all the differentiation rules and formulas. Here, we have differentiated y and x with respect to time, so as to get the rate of decrease of height in m/sec. Sometimes students forget this and differentiate with y with respect to x, this will not lead them to the right answer as there won't be a term indicating the rate of decrease.