Question

A kite is flying with a string of 200m. If the thread makes an angle 30˚ with the ground, find the distance of the kite from the ground level. (Here, assume that the string is along a straight line).

Answer 1

Hint: This problem is based on applications of trigonometry. We will use the trigonometric formula, $\sin \theta =\dfrac{\text{Perpendicular}}{\text{Hypotenuse}}$ to find the height of the kite from the ground. We know that $\sin {{30}^{\circ }}=\dfrac{1}{2}$. So, we get, $\sin {{30}^{\circ }}=\dfrac{1}{2}=\dfrac{\text{height of kite from ground}}{\text{length of string}}$.

Complete step-by-step answer:
It is given in the question that a kite is flying with a string of 200m. And the thread makes an angle 30˚ with the ground, and we have been asked to find the distance of the kite from the ground level.

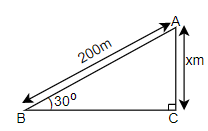
Let us first assume that the height of the kite from the ground is x m. Then, we know the trigonometric formula, $\sin \theta =\dfrac{\text{Perpendicular}}{\text{Hypotenuse}}$. So, we will apply this property in the right angled triangle shown in the figure.
In the right angled triangle ABC, we have,
Perpendicular (AC) = x m
Hypotenuse (BA) = 200 m
So, we can write,
$\sin \theta =\dfrac{\text{Perpendicular}}{\text{Hypotenuse}}.........(i)$
We also know that $\sin {{30}^{\circ }}=\dfrac{1}{2}$. So, on putting the values of perpendicular (AC) = x m, hypotenuse (BA) = 200 m and $\sin {{30}^{\circ }}=\dfrac{1}{2}$ in equation (i), we will get,
$\dfrac{1}{2}=\dfrac{x}{200}$
On cross multiplying the above equation, we will get,
$2x=200$
On dividing the whole equation by 2, we will get,
$\begin{align}
  & x=\dfrac{200}{2} \\
 & x=100m \\
\end{align}$
Therefore, we get the height of the kite, that is, the distance of the kite from the ground as 100m.

Note: The possible mistakes that the students can make while solving this question is that, they may write the value of \[\sin {{30}^{\circ }}=\dfrac{\sqrt{3}}{2}\], this is wrong and students make this mistake as they get confused between the values of sin 30˚ and sin60˚. So, in order to avoid this confusion, the students can use a simple trick, that the value of $\sin \theta $ starts from 0 and it increases up to 1 with the increase of degrees. As 60˚ is greater than 30˚, the value of sin60˚ must be greater than the value of sin30˚, as $\dfrac{\sqrt{3}}{2}>\dfrac{1}{2}$.