Question

A kite is flying at a height of 45m above the ground. The string attached to the kite is temporarily tied to a point on the ground. The inclination of the string with the ground is ${60^ \circ }$. Find the length of the string assuming that there is slack in the string.

Answer 1

Hint: Draw a figure to represent the given situation. In the figure drawn below, the kite is at the height of 45m at point A. String is attached to the ground at point C. So, it forms a triangle ABC, and at C where string is attached forms an angle ${60^ \circ }$ with the ground. We will use $\sin \theta $ for calculating the length of the string because length of the string forms hypotenuse and height of the kite forms perpendicularly. And we know that $\sin \theta = \dfrac{{perpendicular}}{{hypotenuse}}$. So, we will use this formula for getting the length of the string.

Complete step-by-step answer: In the drawn figure, let AC represent length of the string, AB represent height of the kite, ∠ACB = 60°.
          

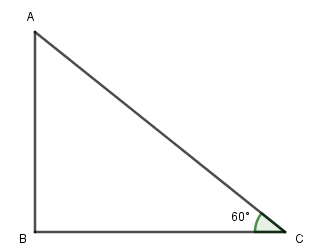
Given,
In $\vartriangle ABC$;
$\angle ACB = {60^ \circ }$(String forms an angle of ${60^ \circ }$from the ground)
AB = 45m (Kite is flying at the height of 45m at point A)
Here, with respect to ∠C, Perpendicular = AB, Base = BC and Hypotenuse = AC.
We know that;
$\sin {60^ \circ } = \dfrac{{perpendicular}}{{hypotenuse}}$
$ \Rightarrow \sin {60^ \circ }$$ = \dfrac{{AB}}{{AC}}$
$ \Rightarrow \dfrac{{\sqrt 3 }}{2} = \dfrac{{45}}{{AC}}$(Value of $\sin {60^ \circ }$is $\dfrac{{\sqrt 3 }}{2}$)
$ \Rightarrow AC = \dfrac{{45 \times 2}}{{\sqrt 3 }} = \dfrac{{90}}{{\sqrt 3 }}$
$ \Rightarrow AC = \dfrac{{90}}{{\sqrt 3 }} \times \dfrac{{\sqrt 3 }}{{\sqrt 3 }} = 30\sqrt 3 $m (Multiplying with $\sqrt 3 $to the numerator and denominator)
Hence, the length of the string = $30\sqrt 3 $m

Note: In the above question we have used a simple formula of trigonometry that is $\sin \theta = \dfrac{{perpendicular}}{{hypotenuse}}$. In trigonometry we have different functions for calculating unknown angles and distances in the geometric figures. There are three basic functions in trigonometry that are sine (sin), cosine (cos), tangent (tan). There are three derived functions : cotangent (cot), secant (sec), and cosecant (cosec). Always be careful while choosing the trigonometric function. First see what parameters are given, then choose the appropriate trigonometric function.