Question

A kite in the shape of a square with a diagonal 32cm and an isosceles triangle of base 8cm and sides 6cm each is to be made of three different shades as shown in figure. How much paper if each shade has been used in it?

Answer 1

Hint: In this, first we find the area of the square using the length of diagonal given in the question. Then, dividing the area of the square by 2, we get the area of each triangle (I and II). Now, we calculate the area of triangle III. By using this methodology, we get how much paper is required.

Complete step-by-step answer:

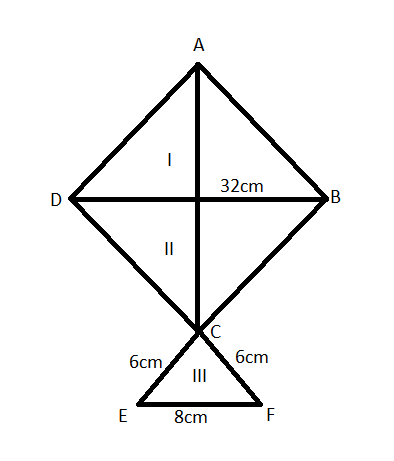
As given in the problem statement, diagonal of square $=32cm$.
Also, base of isosceles triangle$=8cm$.
Also, side of triangle III as per problem $=6cm$.
By using the formula $\dfrac{1}{2}\times {{\left( diagonal \right)}^{2}}$, we calculate the area of square.
Area of the square$=\dfrac{1}{2}\times {{\left( 32 \right)}^{2}}$
Area of the square$=512c{{m}^{2}}$.
From the diagram, Area of triangle I + Area of triangle II = half area of the square $=\dfrac{512}{2}c{{m}^{2}}=256c{{m}^{2}}$.
Area of triangle I and II $=256c{{m}^{2}}$.
$\therefore $Area of paper required triangle I and II $=256c{{m}^{2}}$.
Now,
The Sides of triangle III are 6cm, 6cm and 8cm. The semi-perimeter of triangle is calculated as,
S$=\dfrac{a+b+c}{2}$.
Here, a = 6cm, b = 6cm and c = 8cm.
$\begin{align}
  & S=\dfrac{6+6+8}{2} \\
 & S=\dfrac{20}{2} \\
 & S=10cm \\
\end{align}$
For area of triangle III, we use the Heron’s formula which can be stated as:
$Area=\sqrt{S\left( S-a \right)\left( S-b \right)\left( S-c \right)}$
Now, putting values in the above formula, we get
$\begin{align}
  & Area=\sqrt{10\left( 10-6 \right)\left( 10-6 \right)\left( 10-8 \right)} \\
 & Area=\sqrt{10\times 4\times 4\times 2}c{{m}^{2}} \\
 & Area=4\times 2\sqrt{5}c{{m}^{2}} \\
 & Area=17.92c{{m}^{2}} \\
\end{align}$
Area of paper required for the third triangle is 17.92 square cm.
Therefore, area for paper required for triangle I and II is 256 square cm and for triangle III is 17.92 square cm.

Note: The key concept for solving this question is the knowledge of the area of the square when diagonal is given. Also, Heron's formula is used to evaluate one of the areas of the triangle. These concepts are helpful for solving complex problems.