Question

A Kho-Kho player in a practice session while running realizes that the sum of the distance from the two kho-kho poles from him is always $8\text{m}$.Find the equation of the path traced by him, if the distance between the poles is$6\text{m}$.

Answer 1

Hint: First find the shape of the path by given conditions. Now use the given values to find the values which define that shape. Now using these values try to write the equation of path which is nothing but the required result.

Complete step-by-step answer:
Given the condition in the question is written the sum of distances between poles and man running is always 8m.

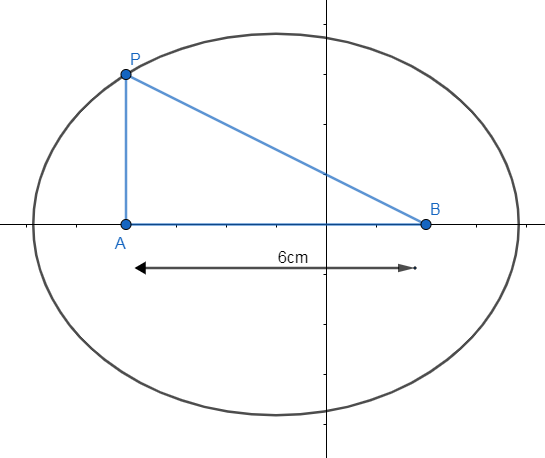
Let the man running be point P which we need.
Let the first pole be assumed to be a point A.
Let the second pole be assumed to be point B.
Given the sum of distance of P from A, B is $8m$, we get: $PA+PB=8m........\left( 1 \right)$.
Given the distance between 2 points A, B is $6m$, we get: $AB=6m.........\left( 2 \right)$.
The sum of the distance from 2 points is a constant and is greater than distance between them. So, this is an ellipse, and positions of poles are foci. Man running is the moving point on the ellipse.
To find an ellipse we need a semi major axis denoted by a, and also a semi minor axis denoted by b.
Relation between b , a is given by eccentricity e in form of: ${{b}^{2}}={{a}^{2}}\left( 1-{{e}^{2}} \right).........\left( 3 \right)$.
Sum of the distance of any point on the ellipse is nothing but the length of the major axis given by$2a$. $PA+PB=2a.$
By substituting the equation $\left( 1 \right)$, we get the equation as: $2a=8.$
By dividing with 2 on both sides, we get it in form of: $a=4..........\left( 4 \right).$
The distance between the foci is nothing but $2a$:$AB=2ae.$
By substituting equation $\left( 2 \right)$ , equation $\left( 4 \right)$, we get it as:$2\left( 4 \right)e=6.$
By dividing with $8$ on both sides, we get it as:$e=\dfrac{6}{8}=\dfrac{3}{4}..........\left( 5 \right).$
Substituting equation$\left( 4 \right),\left( 5 \right)$ in equation$\left( 3 \right)$, we get ${{b}^{2}}={{\left( 4 \right)}^{2}}\left( 1-{{\left( \dfrac{3}{4} \right)}^{2}} \right)=16\left( 1-\dfrac{9}{16} \right).$
By simplifying, we get the value of$\left( b.b \right)$ as given by: ${{b}^{2}}=7.........\left( 6 \right).$
The equation of ellipse is given by: $\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1.$
By substituting equation$\left( 4 \right),\left( 6 \right)$ in the above from, we get:
Therefore the path traced$=\dfrac{{{x}^{2}}}{16}+\dfrac{{{y}^{2}}}{7}=1$ which is an ellipse.

Note: The idea of presenting two poles as two foci and categorize the shape is very important. Don’t confuse between 2a,2ae.Generally students apply formulae in reverse they do 2ae in place of 2a and vice verse which may lead you to the wrong result, formula of b depends whether $e>1,e<1.$If changes with respect to e.