Question

A juggler keeps on moving four balls in the air throwing the balls after regular intervals. When one ball leaves his hand (speed $ = 20m{s^{ - 1}} $ ) , the position of other balls (height in metre) will be : (Take $ g = 10m{s^{ - 2}} $ )
(A) $ 10,20,10 $
(B) $ 15,20,15 $
(C) $ 5,15,20 $
(D) $ 5,10,20 $

Answer 1

Hint :Use the equations of rectilinear motion to find the total time of flight of each ball and find the positions of the balls with respect to the ball in hand .Equations for rectilinear motion under gravitational field is given by, $ h = ut \pm \dfrac{1}{2}g{t^2} $ where, $ u $ is the initial velocity of the object, $ t $ is the total time of fall or fly, $ g $ $ + g $ is the acceleration when the particle is going down. $ - g $ is the acceleration when the particle is going up . $ g = 10m{s^{ - 2}} $ is the acceleration due to gravitational force of attraction.

Complete Step By Step Answer:
We have given that the juggler juggles four balls together and the initial velocity of the balls when it leaves the juggler’s hand is $ 20m{s^{ - 1}} $ . Then, the total time of flight $ t $ of each ball can be found out using, $ h = ut - \dfrac{1}{2}g{t^2} $ where, $ h = 0 $ since the ball goes back and comes back to the hand.
Putting the value of $ u = 20m{s^{ - 1}} $ and $ g = 10m{s^{ - 2}} $ we get ,
 $ 0 = 20t - \dfrac{1}{2}g{t^2} $
Solving this equation we get ,
 $ \dfrac{1}{2}g{t^2} = 20t $
 $ t(gt - 40) = 0 $
 $ gt = 40 $ [ Since, cannot be zero as the ball goes up and come back. ]
Therefore,
 $ t = \dfrac{{40}}{g} = \dfrac{{40}}{{10}} = 4s $ , given $ g = 10m{s^{ - 2}} $
So, each ball goes up and comes back in $ 4s $ . Therefore, after each second one of the balls comes back and the other three remain in the air. So, separation between each ball is $ 1s $ .
So, let's say that at some point, the fourth ball comes back, then the other three must be in the air. So,the third ball already has left the hand $ 1s $ before from the fourth ball. So, the height of it will be the height reached by a particle in $ 1s $ if it were thrown up. Similarly, the second ball has already left the hand $ 2s $ ago, and the first ball has left the hand of the juggler $ 3s $ ago.

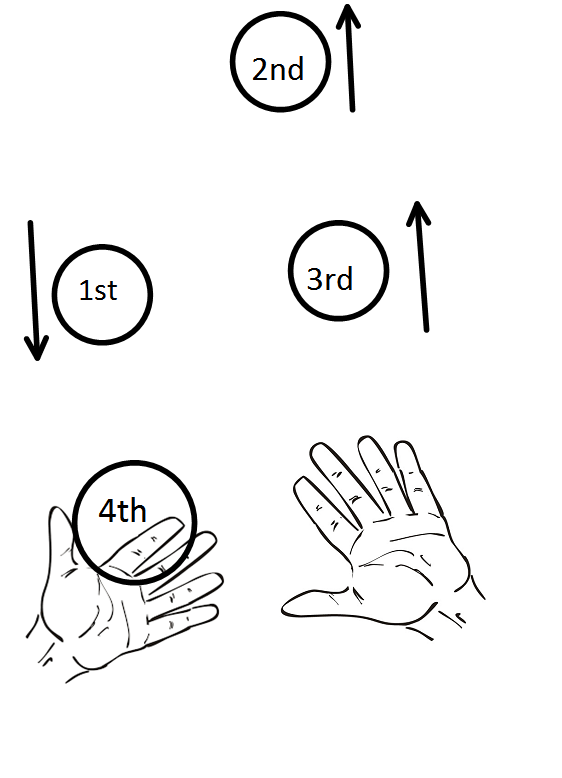
So, we can find the height of each ball by the formula, $ h = ut - \dfrac{1}{2}g{t^2} $
Let’s find the height of each ball: Here for fourth ball $ t = 1s $ and $ u = 20m{s^{ - 1}} $ , $ g = 10m{s^{ - 2}} $ .
Therefore, the height of the third ball will be $ h = 20 \times 1 - \dfrac{1}{2}10 \times {1^2} $ $ h = 20 - 5 = 15m $ from the hand of the juggler.
For second ball: $ t = 2s $ and $ u = 20m{s^{ - 1}} $ , $ g = 10m{s^{ - 2}} $
 $ h = 20 \times 2 - \dfrac{1}{2}10 \times {2^2} $
Or, $ h = 40 - 20 = 20m $
For first ball: $ t = 3s $ and $ u = 20m{s^{ - 1}} $ , $ g = 10m{s^{ - 2}} $
Therefore , $ h = 20 \times 3 - \dfrac{1}{2}10 \times {3^2} $
Or, $ h = 60 - 45 = 15m $
Therefore the balls will be at a separation of $ 15,20,15 $ metre from the hand of the juggler.
Hence, option (B) is correct.

Note :
You can see that when the fourth ball is in hand the first ball is already coming down and will reach his hand by one second.
If the juggler juggles the balls with his two hands but separately ( two separate juggles with two balls each) then the separation between them would be $ 4s $ . You can try the problem.
 To juggle any number of balls the separation of between each ball must be symmetrical else balls cannot be juggled.