Question

A joker’s cap is in the form of a right circular cone of base radius 7 cm and height 24 cm. Find the area of the sheet required to make 10 such caps?

Answer 1

Hint: To find the area of sheet required to make 10 such caps, find the curved surface area of the joker’s cap which is in the form of a right circular cone. The curved surface area of the cone is equal to $\pi rl$ where r is the radius and l is the slant height of the cone. The radius and height of the cone is given. Slant height of the cone is calculated by using Pythagoras theorem. Now, after calculating the curved surface area of 1 cap multiply its result by 10 you will get the area of the sheet.

Complete step-by-step answer:
The joker’s cap is in the form of a right circular cone with radius and height equal to 7 cm and 24 cm respectively. In the below diagram, we have shown the right circular cone.

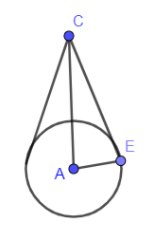
In the above figure, AE is the radius of the cone and AC is the height of the cone.
The curved surface area of the cone is equal to:
$\pi rl$
In the above expression, “r” is the radius of the cone and “l” is the slant height of the cone. Radius of the cone is already given and the slant height of the cone is calculated using Pythagoras theorem.
In $\Delta CAE$, right angled at A we are going to apply Pythagoras theorem.

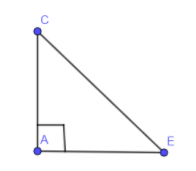
In the above diagram, AE is the radius, CA is the height of the triangle and CE is the slant height of the triangle.
$\begin{align}
  & {{\left( CE \right)}^{2}}={{\left( CA \right)}^{2}}+{{\left( AE \right)}^{2}} \\
 & \Rightarrow {{\left( l \right)}^{2}}={{\left( 24 \right)}^{2}}+{{\left( 7 \right)}^{2}} \\
 & \Rightarrow {{\left( l \right)}^{2}}=625 \\
\end{align}$
Taking square root on both the sides we get,
$l=25$
Hence, the value of slant height is equal to 25 cm.
Now, we can calculate the curved surface area of the cone.
$\begin{align}
  & \pi rl \\
 & =\dfrac{22}{7}\left( 7 \right)\left( 25 \right) \\
 & =22\left( 25 \right)=550 \\
\end{align}$
From the above, the curved surface area of the cone is equal to $550c{{m}^{2}}$.
So, the curved surface area of 10 caps is equal to $5500c{{m}^{2}}$.
Hence, the area of sheet required to make 10 such caps is equal to $5500c{{m}^{2}}$.

Note: The point where you go wrong in the question is writing the value of slant height in the curved surface area formula. In the hastiness of solving the question or a silly mistake you might have written the value of slant height as the height of the cone so beware of making such mistakes in this problem. The mistake of writing slant height as the height of the cone is quite possible because both slant height and height contains the term “height”.