Question

A jet plane is at a vertical height of h. The angles of depression of two tanks on the horizontal ground are found to have measures $ \alpha $ and $ \beta $ . Prove that the distance between the tanks is $ \dfrac{{h\left( {\tan \alpha - \tan \beta } \right)}}{{\tan \alpha \tan \beta }} $ assuming both the tanks are on the same side of the jet plane.​

Answer 1

Hint: Here, draw a diagram based on the information given below. We can see that there are two triangles, find the tangents with respect to the two angles given. Relate the ratio obtained from two triangles, to find the distance between two tanks.

Complete step-by-step answer:
Let A be the position of the plane and C and D be the tanks as shown in the figure

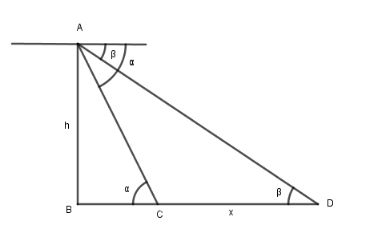
Let the distance between the tanks be x.
Then
In ΔABC
 $ \tan \alpha = \dfrac{{AB}}{{BC}} \Rightarrow \tan \alpha = \dfrac{h}{{BC}} \Rightarrow BC = \dfrac{h}{{\tan \alpha }} $ …(i)
In ΔABD
 $ \tan \beta = \dfrac{{AB}}{{BD}} \Rightarrow \tan \beta = \dfrac{h}{{BC + BD}} $ …(ii)
Putting value BC from (i) in (ii), we have
 $ \tan \beta = \dfrac{h}{{\dfrac{h}{{\tan \alpha }} + BD}} $
On cross-multiplying
 $ \Rightarrow \tan \beta \left( {\dfrac{h}{{\tan \alpha }} + x} \right) = h $
On simplifying
 $ \Rightarrow h\tan \beta + x\tan \alpha \tan \beta = h\tan \alpha $
On rearranging the terms
 $ \Rightarrow x\tan \alpha \tan \beta = h(\tan \alpha - \tan \beta ) $
Finding value of x
 $ \Rightarrow x = \dfrac{{h(\tan \alpha - \tan \beta )}}{{\tan \alpha \tan \beta }} $

Note: In these types of questions, always draw the rough figure; these questions are based on applications of trigonometry. In the above question, height and distance values are not given, so we should try to establish a relation of the value we are to find with values given whether angle or particular length given.
Some important terms:
1. Line of sight or line of vision: A line which is drawn from the eye of an observer to the point in the object where the observer is viewing the object is known as line of sight.
2. Angle of elevation of an object: The angle of elevation of an object is formed by the line of sight with the horizontal when the object lies above the horizontal level.
3. Angle of Depression of an object: The angle of depression of an object is formed by the line of sight with the horizontal when the object lies below the horizontal level.