Question

A jet plane is at a vertical height of $h$. The angles of depression of two tanks on the horizontal ground are found to have measures $\alpha $ and $\beta $, $\alpha > \beta $. Prove that the distance between the tanks is $\dfrac{{h(\tan \alpha - \tan \beta )}}{{\tan \alpha - \tan \beta }}$ assuming both the tanks are on the same side of the jet plane.

Answer 1

Hint: The given question contains the application of trigonometry, known as heights and distances. Also, the angle of depression refers to the angle between the horizontal line and the line of sight of an observer, if its line of sight is below the horizontal.

Complete step by step solution:
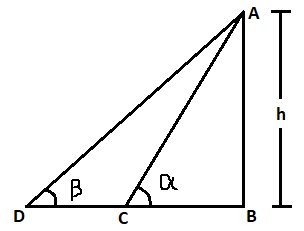
The given question can be made into the diagram given beside.
As the vertical height of the jet plane is $h$, therefore let $AB = h$.
Also, as the angles of depression of the two tanks on the horizontal ground are $\alpha $ and $\beta $, therefore let $\angle ACB = \alpha $ and $\angle ADB = \beta $.
Now for $\Delta ABC$, we have
$\tan \alpha = \dfrac{{AB}}{{BC}}$
On rearranging, we will get
$BC = \dfrac{{AB}}{{\tan \alpha }}$
On putting the value of $AB = h$, we will get
$BC = \dfrac{h}{{\tan \alpha }}$ {equation (1)}
Again for $\Delta ABD$, we have
$\tan \beta = \dfrac{{AB}}{{BD}}$
On rearranging, we will get
$BD = \dfrac{{AB}}{{\tan \beta }}$
On putting the value of $AB = h$, we will get
$BD = \dfrac{h}{{\tan \beta }}$ {equation (2)}
From the figure, it is evident that the distance between the two tanks is $CD$. Also,
$CD = BD - BC$
On substituting equation (1) and equation (2) above, we will get
$ \Rightarrow CD = \dfrac{h}{{\tan \beta }} - \dfrac{h}{{\tan \alpha }}$
$ \Rightarrow CD = \dfrac{{h\tan \alpha - h\tan \beta }}{{\tan \alpha \tan \beta }}$
On factorising $h$ as a common term in the numerator, we will get
$ \Rightarrow CD = \dfrac{{h(\tan \alpha - \tan \beta )}}{{\tan \alpha \tan \beta }}$
Hence, it is proved that the distance between the tanks when both of them are on the same side of the jet plane is given as $\dfrac{{h(\tan \alpha - \tan \beta )}}{{\tan \alpha \tan \beta }}$.

Note:
Before solving the questions containing applications of trigonometry, we must always make the diagram for the given question. It reduces all the confusion and makes the question clearer. Also, we must denote the angle of depression, angle of elevation and one of the length measurements of the triangle (if given) correctly.