Question

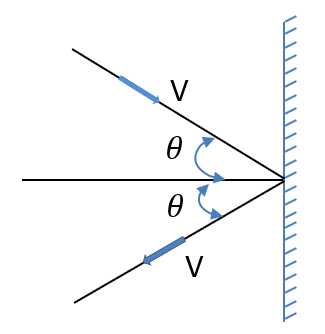
A jet of water with a cross-sectional area $a$ is striking against a wall at an angle $\theta$ to the horizontal and rebounds elastically. If the velocity of the water jet is $v$ and the density is $\rho$, the normal force acting on the wall is:

$A. 2av^2 \rho cos\theta$
$B. av^2 \rho cos\theta$
$C. 2av \rho cos\theta$
$D. av \rho cos\theta$

Answer 1

Hint: Take the differential element of water colliding with a wall and apply the definition of the force as the rate of change of momentum to get the net force acting on the wall.

Complete step-by-step answer:
Let us now consider a small element of water of length dl in the water jet before collision. We are given the area of cross-section as a.

So the small element of volume of water will become $dv = Adl$
We know the density is given by $\rho = \dfrac{m}{V}$
The mass of this small element will become $dm = \rho dv$

Now let us calculate the momentum of this small element before the collision with the wall.

We know the momentum is given by $P = mv$
So the momentum of the small element becomes $dp = vdm = \rho avdl$

This momentum vector is making an angle of $\theta$ degrees with the normal so the horizontal and vertical components of the momentum vector become :

Horizontal component is $dp_(x,i) = dpcos\theta$
The vertical component is $dp_(y,i) = dpsin\theta$

Now after the collision with the wall, the vertical component remains the same, but the horizontal component changes its direction. So the final momentum after collision with the wall becomes :

The final Horizontal component is $dp_(x,f) = - dpcos\theta$
The final Vertical component is $dp_(x,f) = dpsin\theta$

Now the change in momentum has occurred only in the X direction so we can write the change in momentum as : $\Delta dp = dp_(x,f)-dp_(x,i) = 2\rho a vdl cos\theta$

Having got the change in momentum we can now find the force acting on the wall.

We know the force is given by the rate of change of momentum. So we can write $F = \dfrac{dp_x}{dt} = \dfrac{d(2\rho avdl cos \theta)}{dt}$

$F = 2\rho a v^2 cos \theta$ where the velocity is $(v = \dfrac{dl}{dt})$

So we have found the force acting on the wall using the concept of rate of change of momentum and we found force is equal to $2\rho a v^2 cos \theta$ and is acting in the direction of the rate of change of momentum which is perpendicular to the wall.

Note: One of the possible mistakes that we tend to make in this kind of problem is that we calculate the force acting on the wall directly without using the concept of rate of change of momentum which is time-consuming. Another possible mistake can be done while identifying the initial and final momentum before and after collision here we need to understand the angle of incidence and the angle of reflection of the water Jet is the same so only the horizontal component of the momentum changes and the vertical component remains same. These tips will help solve this kind of problem easily.