Question

A jet airplane travelling at a speed of 500 km/h ejects its products of combustion at a speed of 1500 km/h relative to the jet plane. The speed of the latter with respect to an observer on the ground is:
A. 1500km/h
B. 2000km/h
C. 1000km/h
D. 500km/h

Answer 1

Hint: To solve this question one must have the knowledge of relative motions. Use the relative motion formula between two bodies, i.e. ${{\overrightarrow{v}}_{B/A}}=\overrightarrow{{{v}_{B}}}-\overrightarrow{{{v}_{A}}}$. Draw the velocity vectors of the plane and the combustive products and find the value of the $\overrightarrow{{{v}_{B}}}$.

Formula used:
${{\overrightarrow{v}}_{B/A}}=\overrightarrow{{{v}_{B}}}-\overrightarrow{{{v}_{A}}}$

Complete answer:
Let us first understand what is meant by the term relative motion. A relative motion of the body with respect to another body (called an observer) is the motion of that body as seen by the observer.
To understand this let us take an example.
Suppose you and your friend are sitting together in a moving car. When you see your friend, he will be just sitting on the sear and not be moving. This means, according to you, your friend is not moving. However, you are actually moving since you both are sitting inside a moving car.
Therefore, the relative speed of your friend with respect to you is zero (at rest).
On the other hand, your other friend standing nearby on the ground will see you both moving with a speed equal to the speed of the car.
Suppose two bodies A and B are moving with velocities $\overrightarrow{{{v}_{A}}}$ and $\overrightarrow{{{v}_{B}}}$ respectively. These velocities are with respect to the ground (or a stationary observer).
Then the relative motion of A with respect to B is given as ${{\overrightarrow{v}}_{B/A}}=\overrightarrow{{{v}_{B}}}-\overrightarrow{{{v}_{A}}}$.
In the given case, let the velocity of jet be $\overrightarrow{{{v}_{A}}}$ and velocity of products of combustion be $\overrightarrow{{{v}_{B}}}$.

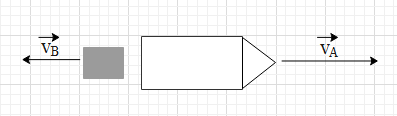
Then $\overrightarrow{{{v}_{A}}}=500km/h$.
It is given that the speed of products of combustion is 1500 km/h relative to the jet plane. From the figure we know that the velocity of $\overrightarrow{{{v}_{B}}}-\overrightarrow{{{v}_{A}}}$ will be in the negative direction.
Hence, ${{\overrightarrow{v}}_{B/A}}=\overrightarrow{{{v}_{B}}}-\overrightarrow{{{v}_{A}}}=-1500km/h$.
Therefore,
$-1500=\overrightarrow{{{v}_{B}}}-500$
$\Rightarrow \overrightarrow{{{v}_{B}}}=-1000km/h$
This means that the speed of the products is 1000km/h with respect to an stationary observer on the ground.
Hence the correct option is C.

Note: There does not exist an absolute motion of a body. This means the motion of every object is relative. We measure the speeds of an object with respect to some observer.
The speeds or velocities that we usually deal with are with respect to the ground. These are not the absolute speeds of the object because the ground is also in motion continuously due to the rotation of earth.