Question

A In the given figure, line I is the bisector of an angle $\angle A$and B is any point on 1. BP and BQ are perpendiculars from B to the arms of $\angle A$. Show that:
$
  i)\vartriangle ABP \cong \vartriangle AQB \\
  ii)BP = BQ \\
 $or B is equidistant from the arms of $\angle A$

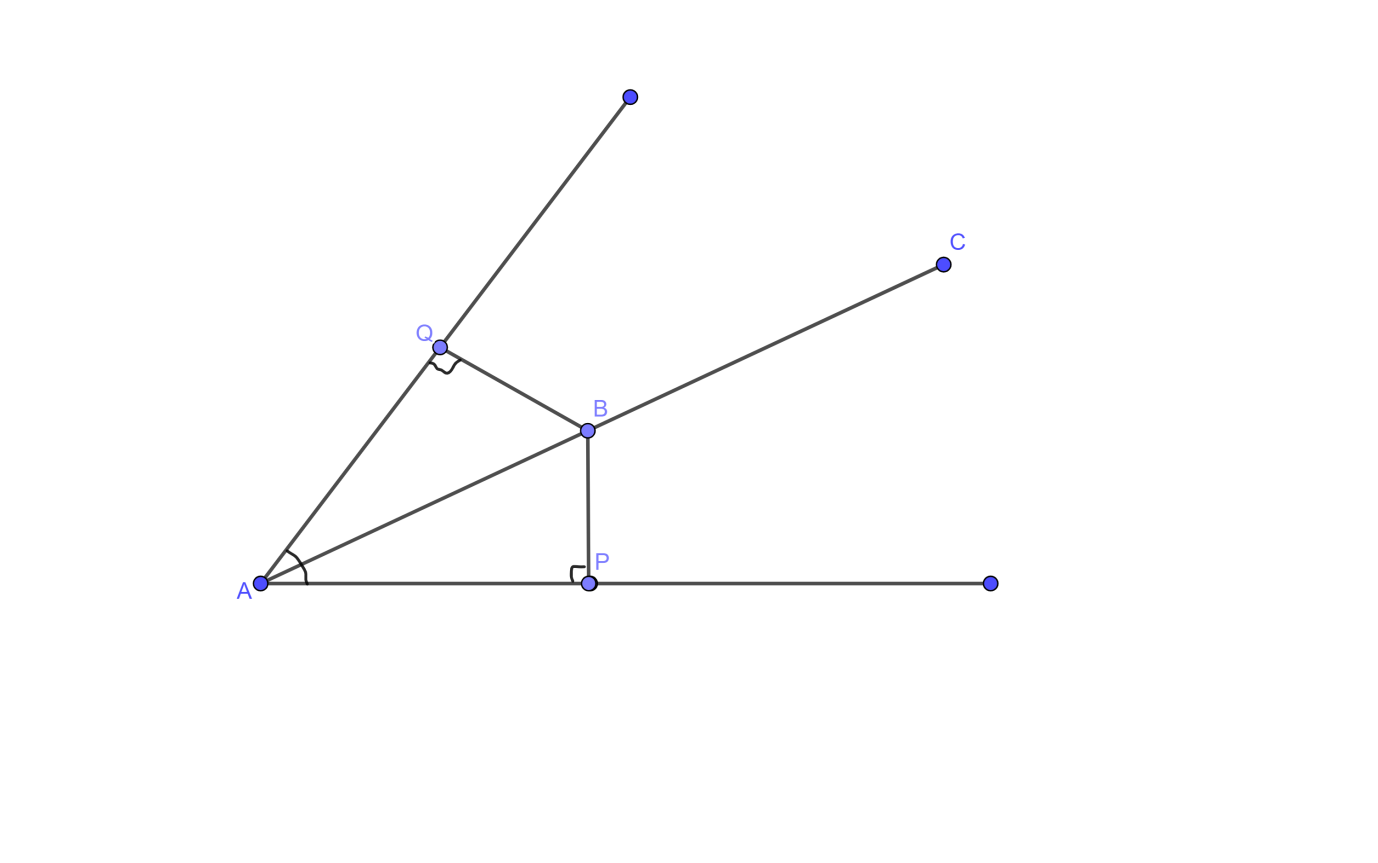
Answer 1

Hint: Use concurrency rules to prove the congruence of the triangles and in the process proves the second half.
First, we consider the bisecting line I and then we get a condition statement and then from observing the diagram we have two right angles. With the help of these two conditions, we prove the congruence between the two triangles. And for the second part, it is easily proved that it is true by corresponding parts of Congruent Triangles. It means that corresponding parts of congruent triangles are equal.

Complete step by step answer:
Since, we are given that line I is the bisector of $\angle A$, it implies that
$\angle PAB = \angle QAB - (1)$
We have the first condition.
Next, we see that BP and BQ are perpendicular, it clearly implies that
$\angle APB = \angle AQB = {90^o} - (2)$
We have the second condition as well.
So, now we shall prove the congruence of the two triangles.
From the second condition, we can say that
$\angle APB = \angle AQB$
And, from the first condition, we can say that
$\angle PAB = \angle QAB$
These two triangles have a common side AB as well.
Hence, we have proved that the two triangles are congruent in nature
$\therefore \vartriangle ABP \cong \vartriangle AQB$
We have proved the congruence by AAS rule, which is Angle Angle Side Rule.
Coming to the second part, the two sides BP and BQ are a part of the congruent triangle.
So, it proved that $BP = BQ$ by the rule of CPCT, corresponding parts of the corresponding triangle.

Note: For CPCT to be applied, it is necessary that the side or anything, both the parts should be part of the triangles which have been proved congruent, or have been given as congruent triangles in the question.