Question

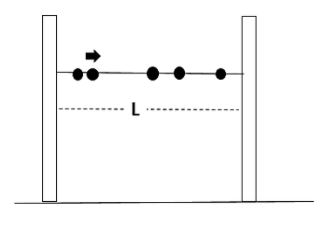
A huge number $\left( n \right)$ of identical beads, each of mass $m$ and radius $r$ are hung on a thin smooth rigid horizontal rod of length $L\left( L >> r \right)$ and are at rest at random positions. The rod is mounted between two rigid supports as shown in the figure. If one of the beads is now given a speed $v$, the average force experienced by each support after a long time will be (assume all collisions are elastic)

$\begin{align}
  & A.\dfrac{m{{v}^{2}}}{L-nr} \\
 & B.\dfrac{m{{v}^{2}}}{L-2nr} \\
 & C.\dfrac{m{{v}^{2}}}{2\left( L-nr \right)} \\
 & D.zero \\
\end{align}$

Answer 1

Hint: First of all find the total length of the string which will be available for the collision. And then calculate the average time required to complete the collision. Note that the collision is given as elastic. Consider the momentum of the bead also and find out the force experienced by each of the supports using the calculated parameters. By this we will get to the answer for this question.

Complete step-by-step answer:
As we know the total length of the string which is available for collision to take place is given as,
$L-nr$
Let us assume that the collision between beads is elastic and each bead comes to rest after collision and the collided beads will move with a velocity $v$.
Therefore the average time taken for collision will be,
${{t}_{avg}}=\dfrac{L-2nr}{v}$
A bead will collide with all other beads before it comes back to the initial state, both in velocity and position, from where it began.
The collision with the support will provide a momentum to the support.
$P=mv$
Therefore the average force felt by the support can be written as,
$F=\dfrac{\Delta P}{\Delta t}$
Substituting the values in it,
$F=\dfrac{mv}{{{t}_{avg}}}$
This can be written as,
$F=\dfrac{mv}{\dfrac{L-2nr}{v}}=\dfrac{m{{v}^{2}}}{L-2nr}$

So, the correct answer is “Option B”.

Note: An elastic collision is given as a collision in which there is no resultant loss in kinetic energy in the system because of the collision. In this collision, both momentum and kinetic energy are conserved quantities. Perfectly elastic collisions are an ideal case.