Question

A horse is placed for grazing inside a rectangular field \[70\]m by \[52\]m and is tethered to one corner by a rope \[21\]m long. How much area can it graze?

Answer 1

Hint:
We consider the corner O is the centre of the circular field. Since the area where the horse can graze is bounded by the length and width of the rectangular field, it is one fourth of the total area of the circular field.
Hence we find the total area of the circle and divide it by four to find the required result.

Complete step-by-step answer:
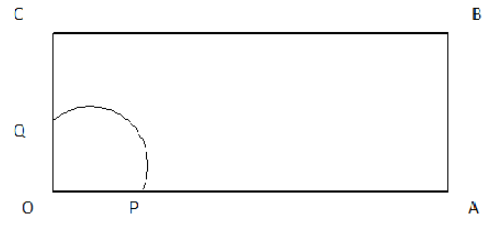
It is given that the length and width of the rectangular field is \[70\]m and \[52\]m respectively. A horse is placed for grazing at a corner O (shown in the diagram). The length of the rope of the horse is \[21\]m.
Now we have to find the area that the horse can graze.
As per the diagram, the horse can graze a circular field of radius of \[21\]m. We consider the corner O is the centre of the circular field. Since the area where the horse can graze is bounded by the length and width of the rectangular field, it is one fourth of the total area of the circular field.
We know that the area of the circle of radius \[r\] is \[\pi {r^2}\]sq. m
Substituting the \[r = 21\] we get, the area of the circular field is \[ = \pi \times 21 \times 21\]sq. m
Solving the above equation by substituting the value of $\pi $ as $\dfrac{{22}}{7}$ we get,
The area is \[1386\]sq. m.
Therefore, the area it can graze is just one fourth of the total area, we get,
The area it can graze \[ = \dfrac{1}{4} \times 1386\]sq. m
Solving the above equation by dividing the term in the denominator we get, the area it can graze \[ = 346.5\]sq. m.
Hence, the area it can graze \[346.5\]sq. m.

Note:
If a horse is tethered at a fixed point, it can move freely in a circular field whose radius is the length of the rope. So we have used the area of the circle of radius r to find the area of field that the horse can graze.