Question

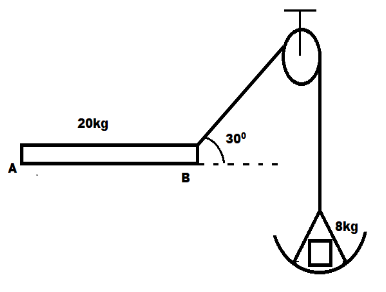
A horizontal uniform beam AB of length 4m and a mass of 20kg is supported at the end B by a ring which passes over a fixed, smooth pulley supporting a counterbalancing weight of 8kg on the other side. What force, F when applied at the point A in a suitable direction, will hold the beam in static equilibrium?
(A) $ F = 160N $
(B) $ F = 40\sqrt {19} N $
(C) $ F = (200 - 80\sqrt 3 )N $
(D) No force F, as specified, can hold the beam in static equilibrium.

Answer 1

Hint :Here in order to find the force required to put the body in equilibrium we should use the force resolution and then balancing force in every direction we can find the required equilibrium force required, here we know that gravitational force, tension in string are acting, since no coefficient of friction is given hence we would not consider friction anywhere.

Complete Step By Step Answer:
Tension T is applied by the pulley upwards on mass 8kg and equal Tension (T) acting towards beam supported at angle 300.
Components are:
 $ \Rightarrow T\sin 30,\,T\cos 30 $
Now we know that from the figure, tension of “sin” component and 8kg mass are in same direction, and gravitational pull on 8kg and 20kg mass are in same direction, now on solving we get:
 $
   \Rightarrow T\sin 30,\,T\cos 30 \\
   \Rightarrow T + T\sin 30 = (20 + 8)g \\
   \Rightarrow T + \dfrac{T}{2} = 28g\,\left( {\sin 30 = \dfrac{1}{2}} \right) \\
   \Rightarrow \dfrac{{3T}}{2} = 28g \\
   \Rightarrow T = \dfrac{{56}}{3}g \\
  $
According to question, the required force “F” is applied at point A, in a suitable direction to hold the beam and is equal to the cosine component of tension force,
 $ \Rightarrow F = T\cos 30 $
Now putting the value of T, we get:
 $
   \Rightarrow F = \dfrac{{56}}{3}g\cos 30 \\
   \Rightarrow F = \dfrac{{56}}{3} \times 9.8 \times \dfrac{{\sqrt 3 }}{2}\left( {g = 9.8(graviatational\,cons\tan t),\cos 30 = \dfrac{{\sqrt 3 }}{2}} \right) \\
   \Rightarrow F = 91.466\sqrt 3 = 40\sqrt {19} \\
  $

Note :
In order to solve the force balancing question we need to solve the body diagram, that is resolving the forces in the horizontal and vertical direction, after making equations of balancing forces, we can obtain the required forces, or any other quantities asked.