Question

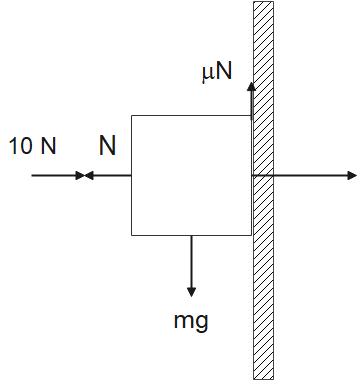
A horizontal force of 10 N is necessary to just hold a block stationary against a wall. The coefficient of friction between the block and the wall is 0.2. Find out the weight of the block.

a.) 50 N
b.) 100 N
c.) 2 N
d.) 20 N

Answer 1

Hint: In this question, we have been asked to find out the weight of the block and we have been given the condition that we need to apply a force of 10 Newton to just make sure that the block does not slip off the wall. We have been given the normal reaction and the force applied to the block and also a diagram of the condition

Complete answer:
In this question, we have been given few quantities such as
Force applied (F) = 10 N
Normal Reaction (R) = 10 N
Frictional Force $f=\mu N$
Where, $\mu $ is the coefficient of friction and “N” is the normal reaction which in this question is shown as “R”
$\mu $ = 0.2
Now, we know that the force applied is balanced by the normal reaction
Therefore, we can say,
F = R
Or, 10N = R (because Force applied (F) = 10 N )
Therefore, Normal Reaction (R) =10 N
Now, the frictional force $f=\mu N$ is balanced by the weight “mg”
$\mu N=mg$
Putting the values, of $\mu $ , N
We get,
$(0.2)(10)=mg$
mg = 2 N
Therefore, Weight of the block is 2 Newton

Hence, we can conclude that option (c) is the correct answer.

Note:
Frictional force always acts opposite to the direction of motion, hence in this figure the frictional force totally balances the weight of the body which makes it totally stable and it does not slip off the downside. If the force of gravity or weight is stronger than the block will move in the downward direction because the forces will not be balanced.