Question

A horizontal force, just sufficient to move a body of mass 4 kg lying on a rough horizontal surface is applied on it. The coefficients of static and kinetic friction between the body and the surface are 0.8 and 0.6 respectively. If the force continues to act even after the block has started moving, the acceleration of the block in $m{{s}^{-2}}$ is ($g=10m{{s}^{-2}}$)
$\left( A \right)0.25$
$\left( B \right)0.5$
$\left( C \right)2$
$\left( D \right)4$

Answer 1

Hint: As there is the application of the force on an object of mass 4 kg so, we will apply the formula of static and frictional forces along with the force as a product of mass and acceleration. With the help of these formulas we will be able to find acceleration.

Formula used:
${{F}_{static}}={{\mu }_{static}}\times mass\times g,{{F}_{friction}}={{\mu }_{friction}}\times mass\times g,Total\,force={{F}_{static}}-{{F}_{friction}}$ and $Total\,force=ma$ where m is the mass and a is the acceleration. Also, ${{F}_{friction}}$ is the frictional force, ${{F}_{static}}$ is static force. And g is the force of gravity.

Complete answer:

Static force: It is a type of force with the help of which any object remains at rest. It is actually a force with equal and opposite force applied against the force which makes the object to move. The diagram showing this force is shown below.

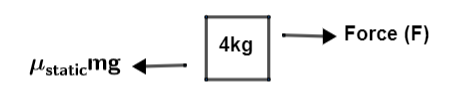
As it is given that the mass of the object to which the static force is applied is given as 4 kg. The static force applied here has the value of 0.8 along with the gravitational force as $g=10m{{s}^{-2}}$. To find the force here, we will use formula ${{F}_{static}}={{\mu }_{static}}\times mass\times g$ and substitute the values in it. This result into,
$\begin{align}
  & {{F}_{static}}={{\mu }_{static}}\times mass\times g \\
 & \Rightarrow {{F}_{static}}=0.8\times 4\times 10N \\
 & \Rightarrow {{F}_{static}}=8\times 4N \\
 & \Rightarrow {{F}_{static}}=32N \\
\end{align}$


Frictional force: It is the force in which the object performs motion after coming in contact with another object. The diagram showing this force is shown below.

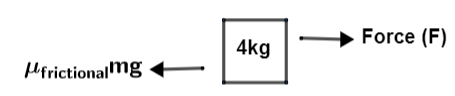
As it is given that the mass of the object to which the frictional force is applied is given as 4 kg. The frictional force applied here has the value of 0.6 along with the gravitational force as $g=10m{{s}^{-2}}$ . To find the force here, we will use formula ${{F}_{friction}}={{\mu }_{friction}}\times mass\times g$ and substitute the values in it. This result into,
$\begin{align}
  & {{F}_{friction}}={{\mu }_{friction}}\times mass\times g \\
 & \Rightarrow {{F}_{friction}}=0.6\times 4\times 10N \\
 & \Rightarrow {{F}_{friction}}=6\times 4N \\
 & \Rightarrow {{F}_{friction}}=24N \\
\end{align}$
Now, the total force here will be $Total\,force={{F}_{static}}-{{F}_{friction}}$ and $Total\,force=ma$ so, we have
$\begin{align}
  & {{F}_{static}}-{{F}_{friction}}=ma \\
 & \Rightarrow 32-24=\left( 4 \right)a \\
 & \Rightarrow a=\dfrac{8}{4} \\
 & \Rightarrow a=2 \\
\end{align}$
Therefore, the acceleration is $2m{{s}^{-2}}$.

So, the correct answer is “Option C”.

Note:
To solve these types of questions we will learn the following points effectively,
(1) Static force is always greater than frictional force or kinetic force.
(2) The force should be calculated in Newton as Newton is the SI unit of force.
(3) The gravitational force is present on all the objects that are present around us. The general value of this force is $9.8m{{s}^{-2}}$ but since, we are given the value as $g=10m{{s}^{-2}}$ in this question, this is why we have used it. Otherwise, if the value of g is not specifically given in the question so, always use g as $9.8m{{s}^{-2}}$.