Question

A hollow square-shaped tube open at both ends is made of iron. The internal square is 5cm and the length of the tube is 8cm. There is $ 192c{{m}^{2}} $ of iron in this tube. Find its thickness.

Answer 1

Hint: Start by letting the thickness of the tube be t cm. So the side length of the outer surface becomes (5+2t) cm. Find the volume of the inner cuboid and subtract it from the volume of the outer cuboid and equate the result with the volume of the iron to get the thickness. Remember that volume of the cuboid is base area multiplied by height, i.e., $ {{a}^{2}}l $ , where a is the side length of the base which is a square and l is the length.

Complete step-by-step answer:
To start with the question let us draw the diagram of the tube. We let the thickness of the tube be t.

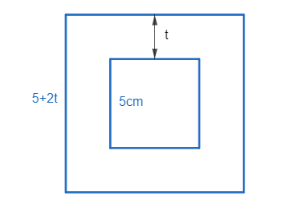
The above diagram shows the view of the tube if we see it from one end.
Now first let us find the inner volume of the cuboidal tube. It is given that the inner side length of the base is 5 cm and length of the tube is 8cm. We also know that that volume of the cuboid is base area multiplied by height, i.e., $ {{a}^{2}}l $ , where a is the side length of the base which is a square and l is the length.
 $ \text{Inner volume =}{{\text{a}}^{2}}l={{5}^{2}}\times 8=200c{{m}^{3}} $ .
Also, the outer volume can be found using the outer side length of the base, which is equal to (5+2t) cm. l in this case also remains the same.
 $ \text{Outer volume}={{a}^{2}}l={{\left( 5+t \right)}^{2}}\times 8 $
We can also see from the figure the volume of the tube is inner volume subtracted from the outer volume, as inner volume is hollow and it is given in the question that volume of the iron is $ 192c{{m}^{3}} $ . So, using the above results we can say that:
\[\text{Volume of iron tube}=8\times {{\left( 5+2t \right)}^{2}}-200\]
 $ \Rightarrow 192=8\times {{\left( 5+2t \right)}^{2}}-200 $
 $ \Rightarrow 392=8\times {{\left( 5+2t \right)}^{2}} $
 $ \Rightarrow 49={{\left( 5+2t \right)}^{2}} $
Now, if we take square root of both the sides of the equation, we get
  $ \sqrt{49}=\sqrt{{{\left( 5+2t \right)}^{2}}} $
We know 49 is the square of 7.
 $ 7=5+2t $
 $ \Rightarrow 2t=2 $
 $ \Rightarrow t=1\text{ cm} $
Therefore, the answer to the above question is 1cm.

Note: You could have solve the last part of the equation by using the formula of $ {{\left( a+b \right)}^{2}} $ to convert the equation $ 49={{\left( 5+2t \right)}^{2}} $ into a quadratic equation and use the quadratic formula to get the roots, but that method would be lengthy and time taking. Also, remember that all cuboids are prisms, hence, we have used the formula that volume is equal to length times the base area.