Question

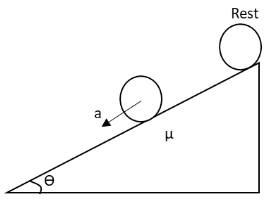
A hollow sphere starts pure rolling from rest as shown. The acceleration of centre of mass of sphere is

A. \[\dfrac{1}{5}g\sin \theta \]
B. \[\dfrac{2}{5}g\sin \theta \]
C. \[\dfrac{3}{5}g\sin \theta \]
D. \[\dfrac{4}{5}g\sin \theta \]

Answer 1

Hint: Use the formulae for the torque acting on an object due to a force and also in terms of angular acceleration. Calculate the net torque acting on the hollow cylinder about an axis at the point of contact of the sphere and inclined plane. Use the value of moment of inertia of the cylinder about an axis passing through this point of contact.

Formulae used:
The torque \[\tau \] acting on an object due to a force \[F\] is
\[\tau = Fr\] …… (1)
Here, \[r\] is the perpendicular distance between the point of action of the force and centre of torque.
The torque \[\tau \] acting on an object is
\[\tau = I\alpha \] …… (2)
Here, \[I\] is the moment of inertia of the object and \[\alpha \] is angular acceleration of the object.
The moment of inertia \[I\] of a hollow sphere about an axis passing through a point on the circumference of the sphere and parallel to its diameter is
\[I = \dfrac{5}{3}m{R^2}\] …… (3)
Here, \[m\] is the mass of the hollow sphere and \[R\] is radius of the hollow sphere.
The relation between the linear acceleration \[a\] and angular acceleration \[\alpha \] is
\[a = R\alpha \] …… (4)
Here, \[R\] is the radius of the circular path.

Complete step by step answer:
We have given that a hollow sphere is rolling down an inclined plane. Let us draw a free body diagram of the cylinder.

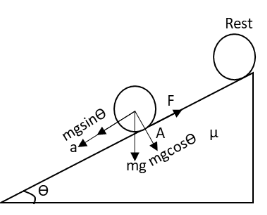
Let \[m\] be the mass of the hollow cylinder and \[R\] be the radius of the hollow sphere.We can calculate the net torque on the hollow cylinder about an axis passing through point A.The torque due frictional force and vertical component of weight of the hollow sphere about an axis passing through the point A is zero.The net torque is only due to the horizontal component \[mg\sin \theta \] of the weight of cylinder.

Substitute \[mg\sin \theta \] for \[F\] and \[R\] for \[r\] in equation (1).
\[\tau = \left( {mg\sin \theta } \right)R\]
Substitute \[I\alpha \] for \[\tau \] in the above equation.
\[I\alpha = \left( {mg\sin \theta } \right)R\]
Substitute \[\dfrac{5}{3}m{R^2}\] for \[I\] and for \[\alpha \] in the above equation.
\[\dfrac{5}{3}m{R^2}\dfrac{a}{R} = mgR\sin \theta \]
\[ \therefore a = \dfrac{3}{5}g\sin \theta \]
Therefore, the acceleration of the centre of mass of the hollow cylinder is \[\dfrac{3}{5}g\sin \theta \].

Hence, the correct option is C.

Note:The students should be careful while using the value of moment of inertia of the hollow cylinder in the formula for torque. The students should keep in mind that we are calculating the torque about the point A. Hence, the moment of inertia of the hollow cylinder should also be calculated about the axis passing through the point A and not through the centre.