Question

A hollow metal sphere of radius 20cm is charged such that the potential on its surface is \[120V\] . The potential at the center of the sphere is

Answer 1

Hint: The potential is constant throughout the volume of the hollow metallic sphere.
here no electrical field is present inside a metal body of any shape, even a hollow one.
electrostatic voltage is described as the work done per coulomb against the electric field to move a charge from an infinite distance.

Complete answer:

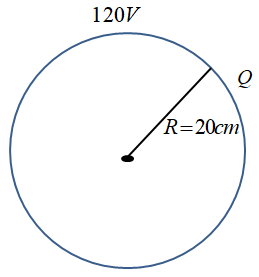
We already know, the electric potential of any point on the surface or inside a solid or hollow metallic sphere of radius \[R\] & having charge \[Q\] uniformly distributed on the surface is given as
\[V = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{Q}{R} = \dfrac{{\sigma R}}{{{\varepsilon _0}}}\]
Where, \[\sigma = \dfrac{Q}{{4\pi R2}}\] is the uniform surface charge density
Hence, when the potential on a sphere is \[120V\] then the potential at the center or any other interior point will be \[120V\] because when we charged a metallic sphere then the charge is distributed over its surface uniformly that is there is a zero charge inside it hence there are zero electric fields inside the metallic sphere but the electric potential remains constant inside it.
Finally, the Potential inside the charged sphere is constant and equal to potential on the surface. Here, the potential at the center is \[120V\] .

Note:
As the sphere is generally made up of metal here, it is conducting so there is no electric field inside the sphere so there will be no change in potential from surface to any point inside the sphere.
Here, The potential at the center point is the same.
Usually, The potential inside any hollow metal and the surface same.