Question

A hollow garden roller of 42 cm diameter and length 152 cm is made of cast iron 2 cm thick. Find the volume of iron used in the roller.

Answer 1

Hint: Here the question is related to the mensuration topic. We have to determine the volume of the hollow garden roller which is in the shape of a hollow cylinder. This can be determined by using the formula \[V = \pi \left( {{R^2} - {r^2}} \right)h\] cubic units, where \[R\] and \[r\] represents the external and internal radius a cylinder respectively.

Complete step by step solution:
Hollow cylinder a cylinder that is empty from the inside and has some thickness at the peripheral or outside. The shape formed at the bottom of a hollow cylinder is called an annular ring, i.e., it is a region bounded by two concentric circles.
The volume of the hollow cylinder is equal to \[V = \pi \left( {{R^2} - {r^2}} \right)h\] cubic units.
Now consider the given question
Given a hollow garden roller which is similar to the shape of a hollow cylinder of 42 cm diameter and length of 152 cm is made up of cast iron 2 cm thick.
 

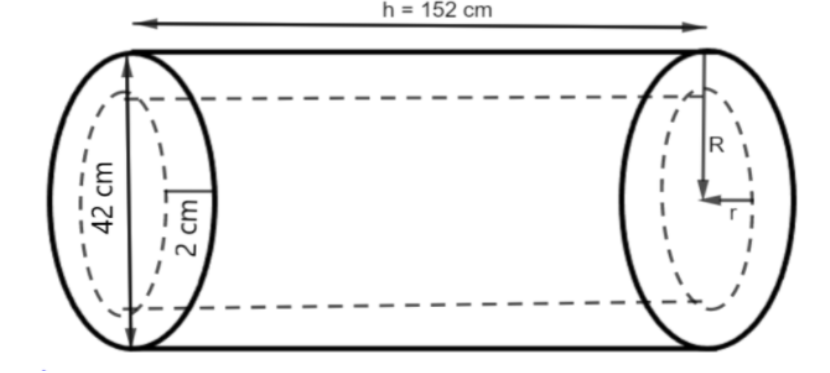
The width of a hollow cylinder = 2 cm.
The diameter of a hollow cylinder = 42 cm.
The radius of a hollow cylinder = \[\dfrac{{42}}{2}\, = \,21\] cm.
The external radius of the hollow cylinder is represented as \[R\]
Therefore \[R = 21\,cm\]
Now we have to determine the inner radius of the hollow cylinder. So, we have to the subtract the width from external radius of hollow cylinder
So, we have
 \[r = R - w\]
On adding we have
 \[ \Rightarrow r = 21 - 2 = 19cm\]
Therefore, the internal radius of hollow cylinder is represented \[r\] and its value is \[r = 19cm\]
The height of the hollow cylinder \[h = 152\,cm\]
The volume of a hollow cylinder is given by \[V = \pi \left( {{R^2} - {r^2}} \right)h\]
On substituting the values, we have
 \[ \Rightarrow V = \pi \left( {{{21}^2} - {{19}^2}} \right)152\]
On simplifying we have
 \[ \Rightarrow V = \pi \left( {441 - 361} \right)152\]
 \[ \Rightarrow V = \pi \left( {80} \right)152\]
Take \[\pi = \dfrac{{22}}{7}\] , on substituting the value of pi
 \[ \Rightarrow V = \dfrac{{22}}{7} \times \left( {80} \right) \times 152\]
 \[ \Rightarrow V = \dfrac{{267520}}{7}\]
On simplifying we have
 \[ \Rightarrow V = 38217.14\,\,c{m^3}\]
Therefore, the volume of the hollow garden roller is \[38217.14\,\,c{m^3}\] .
So, the correct answer is “ \[38217.14\,\,c{m^3}\] ”.

Note: Cylinder or hollow cylinder is a three- dimensional shape. Remember, volume means we need to calculate the amount of space occupied by a three-dimensional object or region of space, when we find any type of measurement we have to mention the units. The unit for the volume is cubic units.