Question

A hollow cylinder with both sides open generates a frequency of \[f\]in air. When cylinder vertically immersed into water by half its length then frequency will be
a) \[f\]
b) \[2f\]
c) \[\dfrac{f}{2}\]
d) \[\dfrac{f}{4}\]

Answer 1

Hint: Since here it is not given which mode it is talking of so we will take default or fundamental frequency for the open hollow cylinders.

Formula Used:
1.Fundamental frequency of pipe which has both ends open: \[f = \dfrac{v}{{2L}}\] …… (A)
Where, \[v\]is the velocity of sound in air and \[L\]is length of air column in the pipe.
2. Fundamental frequency of pipe which has just one of the ends open: \[{f_1} = \dfrac{v}{{4L}}\]
Where, \[v\]is velocity of sound in air and \[L\]is length of air column in the pipe.
3. Nearest distance between antinode and node: $\dfrac{\lambda }{4}$ …… (B)
Where, $\lambda $ is the wavelength of sound.
4. Relation between speed, wavelength and frequency of sound: \[f = \dfrac{v}{\lambda }\] …… (C)

Complete step by step answer:
Given, just fundamental frequency of hollow cylinder both ends open: \[f\]
Let say, \[v\] be the velocity of sound in air and L be the length of pipe or cylinder.
\[{f_{new}}\] be a new frequency when half immersed in water.
Diagram: Below would show fundamental mode setup in two cases:

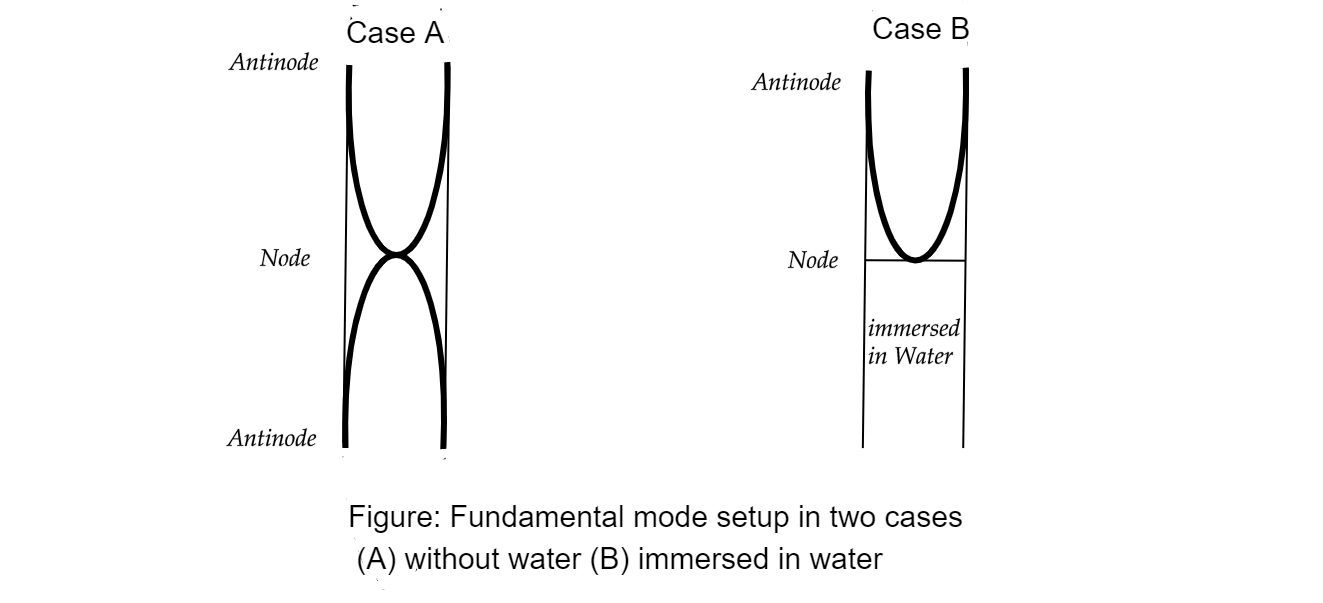
Step 1:
Open end of the pipe acts as an antinode and the closed end as a node.
Case 1: Both ends open
Therefore, in case of both ends open:
$\dfrac{\lambda }{4} + \dfrac{\lambda }{4} = L$
$ \Rightarrow \dfrac{\lambda }{2} = L \Rightarrow \lambda = 2L$ …… (1)
From equation (c) and (1)
We get fundamental frequency to be: \[f = \dfrac{v}{\lambda }\]\[ \Rightarrow f = \dfrac{v}{{2L}}\] …… (2)
Step 2:
Case 2: One end closed:
Here, Water boundaries act as nodes and open-end act as antinodes. And the length of the air column reduces to $\dfrac{L}{2}$.
Distance between antinode to node: $\dfrac{{{\lambda _1}}}{4} = \dfrac{L}{2}$ …… (3)
Using equation (C) and (3) we get new frequency to be: \[ \Rightarrow {f_1} = \dfrac{v}{\lambda } \Rightarrow {f_1} = \dfrac{v}{{2L}}\] …… (4)
Step 3:
Comparing equation (2) and (4) we get: \[ \Rightarrow f = {f_1} = \dfrac{v}{{2L}}\]
Correct Answer:
Option : a)\[f\]

Note:
1. Velocity of sound is constant in a given isotropic media.
2. The first fundamental mode is the longest wavelength possible for the standing wave that can be setup in a given air column.