Question

A hollow cylinder having external radius 8cm and height 10cm has a total surface area of $338\pi c{m^2}$. Find the thickness of the hollow metallic cylinder.
A) $2cm$
B) $3cm$
C) $4cm$
D) $5cm$

Answer 1

Hint: According to the question given in the question we have to determine the thickness of the hollow metallic cylinder when a hollow cylinder having external radius 8cm and height 10cm has a total surface area of $338\pi c{m^2}$. So, first of all we have to let the internal radius of the hollow cylinder but as we know that the total surface area of the cylinder given is $338\pi c{m^2}$ hence, we have to use the formula to find the total surface area of the cylinder which is given below:
Total surface area for the given cylinder = Area of external cylinder + Area of internal cylinder + Area of twice base rings

Formula used: $ \Rightarrow 2\pi R + 2\pi r + 2\pi ({R^2} - {r^2})..................(A)$
We can also understand the perimeters with the help of the diagram as mentioned below:

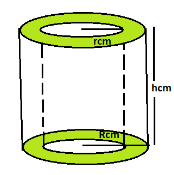
Where, r is the internal radius and R is the external radius.
Hence, on substituting all the values in the expression we can easily obtain the required thickness of the hollow metallic cylinder.
Now, to obtain the thickness of the hollow cylinder can be obtained by subtracting the internal radius which is r by the external radius which is R.

Complete step-by-step answer:
Given,
External radius 8cm and height 10cm,
Total surface area = $338\pi c{m^2}$
Step 1: First of all to find the thickness of the hollow metallic cylinder we have to let the internal radius of the given hollow cylinder. Hence,
Let the internal radius of the hollow cylinder = r cm
Step 2: Now, we have to use the formula (A) to find the total surface area as mentioned in the solution hint.
\[ \Rightarrow 2\pi R + 2\pi r + 2\pi ({R^2} - {r^2}) = 38\pi \]
Step 2: Now, we have to take $2\pi $ as a common term in the expression as obtained in the solution step 1. Hence,
\[ = 2\pi (Rh + rh + {R^2} - {r^2}) = 338\pi \]…………………..(1)
Step 3: Now we have to substitute all the perimeters in the expression (1) as obtained in the solution hint. Hence,

$ \Rightarrow (10 \times 8) + (10 \times r) + {(8)^2} - {r^2} = \dfrac{{338\pi }}{{2\pi }}$
Now, on solving the terms as obtained in the right side of the expression just above by eliminating $\pi $ and dividing 338 by 2,
$
   \Rightarrow (80) + (10r) + 64 - {r^2} = 169 \\
   \Rightarrow - {r^2} + 10r = 169 - 144 \\
   \Rightarrow - {r^2} + 10r = 25...............(2)
 $
Step 4: Now, we have to rearrange the terms of the expression (2) as obtained in the solution step 3 by multiplying with negative sign in the both sides of the expression,
$ \Rightarrow {r^2} - 10r + 25 = 0$
Step 5: Now, to solve the expression as obtained in the solution step 4, we have to find the factors of 25 for the expression to obtain its roots. Hence,
$
   \Rightarrow {r^2} - (5 + 5)r + 25 = 0 \\
   \Rightarrow {r^2} - 5r - 5r + 25 = 0 \\
   \Rightarrow r(r - 5) - 5(r - 5) = 0 \\
   \Rightarrow (r - 5)(r - 5) = 0
 $
Step 6: Now, from the solution step 5 we can obtain both of the roots which is solved below:
$
   \Rightarrow (r - 5) = 0 \\
   \Rightarrow r = 5
 $
Step 7: Now, as we know that the thickness of the hollow cylinder can be obtained by subtracting internal radius which is r by the external radius which is R as mentioned in the solution hint. Hence,
Thickness of metal $ = R - r$
On substituting the values in the expression above,
$ \Rightarrow (8 - 5) = 3cm$
Final solution: Hence, with the help of the formula (A) above, we have obtained the thickness of the hollow metallic cylinder which is equal to $3cm$.

Therefore option (B) is correct.

Note: It is necessary to find the area of twice base rings to obtain the value of total surface area of the given hollow cylinder because base and upper rings are also the parts of that given hollow cylinder.
For a quadratic expression we will always obtain two roots and they can be obtained by finding the factors of the given constant term in that quadratic expression/equation.