Question

A hemispherical bowl has a diameter of 9 cm. The liquid is poured into cylindrical bottles of diameter 3 cm and height 3 cm. If a full bowl of liquid is filled in the bottles, find how many bottles are required.

Answer 1

Hint: In this question the basic idea is that the volume of the liquid remains unchanged before and after the transferring i.e. volume of liquid before transferring=volume of liquid after transferring. Hence, the number of items required to completely empty the vessel can be found.

Complete step-by-step solution:

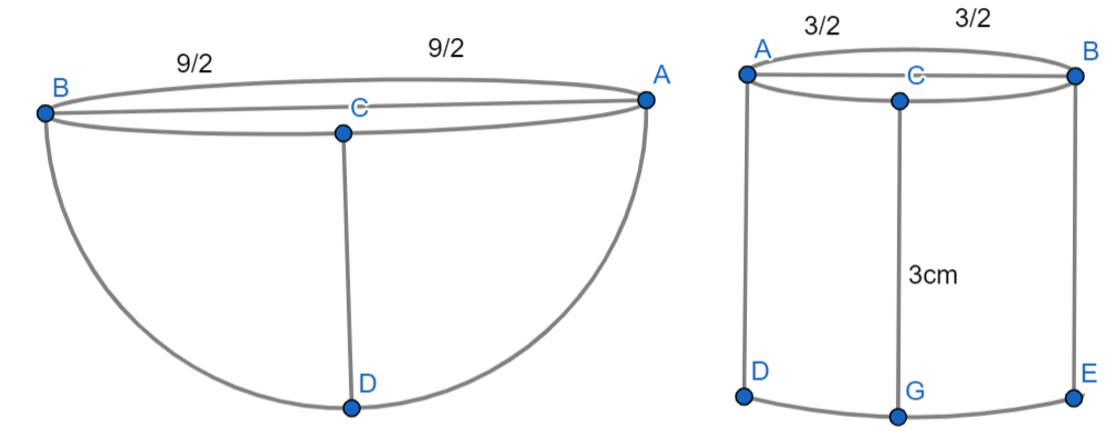
Given,
${\text{Diameter of the hemispherical bowl = 9 cm}}$
${\text{Diameter of the cylindrical bottle = 3 cm}}$
$\because {\text{Radius = }}\dfrac{{{\text{diameter}}}}{2}$
$ \Rightarrow {\text{Radius of the hemispherical bowl = }}\dfrac{{\text{9}}}{2}{\text{ cm}}$
${\text{radius of the cylindrical bottle = }}\dfrac{3}{2}{\text{cm}}$
${\text{height of the cylindrical bottle = 3 cm}}$
$\because {\text{Volume remains constant}}$
${\text{Volume of hemisphere = }}\dfrac{2}{3}\pi {R^3}$
Where R is the radius of the hemisphere.
\[{\text{Volume of cylindrical bottle = }}\pi {r^2}h\]
Let n be the total number of bottles required,
$\because {\text{ Volume remains constant}}$
$\therefore {\text{Volume of water in hemispherical bowl = volume of water in cylindrical bottles}}$
$ \Rightarrow \dfrac{2}{3}\pi {R^3} = n \times \pi {r^2}h$
On dividing both sides by $\pi $ ,
$ \Rightarrow \dfrac{2}{3}{R^3} = n \times {r^2}h$
On dividing both sides by ${r^2}h$,
$ \Rightarrow \dfrac{{2{R^3}}}{{3{r^2}h}} = n$
Or,
$ \Rightarrow n = \dfrac{{2{R^3}}}{{3{r^2}h}}$
On putting the values of R, r and h,
$ \Rightarrow n = \dfrac{{2 \times {{\left( {\dfrac{9}{2}} \right)}^3}}}{{3 \times {{\left( {\dfrac{3}{2}} \right)}^2} \times 3}}$
$ \Rightarrow n = \dfrac{{2 \times \dfrac{9}{2} \times \dfrac{9}{2} \times \dfrac{9}{2}}}{{3 \times \dfrac{3}{2} \times \dfrac{3}{2} \times 3}}$
On multiplying the numerator and denominator by $2 \times 2 \times 2$ in RHS,
$ \Rightarrow n = \dfrac{{2 \times \dfrac{9}{2} \times \dfrac{9}{2} \times \dfrac{9}{2} \times 2 \times 2 \times 2}}{{3 \times \dfrac{3}{2} \times \dfrac{3}{2} \times 3 \times 2 \times 2 \times 2}}$
On simplifying further,
\[ \Rightarrow n = \dfrac{{2 \times 9 \times 9 \times 9}}{{3 \times 3 \times 3 \times 3 \times 2}}\]
On dividing numerator and denominator by 2,
\[ \Rightarrow n = \dfrac{{\dfrac{{2 \times 9 \times 9 \times 9}}{2}}}{{\dfrac{{3 \times 3 \times 3 \times 3 \times 2}}{2}}}\]
On simplifying further,
\[ \Rightarrow n = \dfrac{{9 \times 9 \times 9}}{{3 \times 3 \times 3 \times 3}}\]
On simplifying further,
\[ \Rightarrow n = \dfrac{{729}}{{81}}\]
On dividing,
$n = 9$
$\therefore $ 9 bottles are required to completely empty the hemispherical vessel.

Note: Calculations should be done carefully to avoid any mistake. If n comes out to be a natural number then we can say that all the volume of the liquid is poured to the desired container but if n comes to fraction then all the volume of the material cannot be poured into the desired material and some part of the material remains not poured. Always try to solve the problem step by step so that the wrong step can be determined and changed accordingly. The formula for the volume of that substance should be known such as if the material to be poured is spherical then the volume of sphere should be known which is $\dfrac{4}{3}\pi {r^3}$ where r is the radius of the sphere. All the units should be in the same units and diameter is to be converted into radius.