Question

A heavy ring of mass m is clamped on the periphery of a light circular disc. A small particle having equal mass is damped at the centre of the disc. The system is rotated in such a way that the centre moves in a circle of radius r with a uniform speed \[v\] . We conclude that the external force …
A. \[\dfrac{{m{v^2}}}{r}\] ,Must be acting on the central particle.
B. \[\dfrac{{2m{v^2}}}{r}\] ,Must be acting on the central particle.
C. \[\dfrac{{2m{v^2}}}{r}\] ,Must be acting on the system.
D. \[\dfrac{{m{v^2}}}{r}\], Must be acting on the ring.

Answer 1

Hint: To find out the force on the system of particles , first treat the bodies of the system as a whole system then apply the formula on the centre of mass of the system. Here total of mass 2m is moving with velocity ( v ) so the centrifugal force on the system of particle is \[{F_C} = \dfrac{{{m_{system}}{{(velocity)}^2}}}{{radius\;ofc.o.m}}\].

Complete Step by step solution :
The situation is shown here

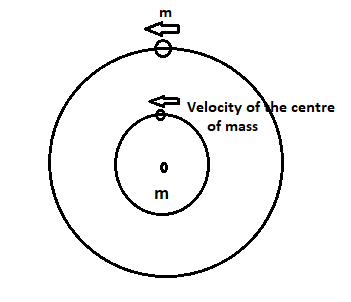
\[{F_C}\]

Let us consider the heavy ring of mass m is clamped on the periphery of a light circular disc and a small particle having equal mass is damped at the centre of the disc as a system. Then the centre of mass of the system has a total of mass 2m.

Now, it is given that the centre of mass moves with velocity v in a circle , so due to this circular motion of the centre of mass there will be a centrifugal force .
\[ \Rightarrow {F_C} = \dfrac{{{m_{system}}{{(velocity)}^2}}}{{radius\;ofc.o.m}}\]
Putting the values \[{m_{system}} = 2m\]; \[velocity = v\]; \[radius\;ofc.o.m = r\]
\[ \Rightarrow {F_C} = \dfrac{{2m{v^2}}}{r}\]
Since, \[\dfrac{{2m{v^2}}}{r}\] ,Must be acting on the system as a centrifugal force ,

Hence option ( C ) is the correct answer.

Note:
When a body moves in a circular motion there acts a force due to which the particle still continues its path in a circle and this force is constant in nature if the velocity of the body is constant and called as centripetal force.
The value of the centripetal force is
\[{F_{centripetal}} = \dfrac{{{m_{body}}{{(velocity)}^2}}}{{radius\;of circle}}\].