Question

A heavy iron bar of weight $W$ is having its one end on the ground and the other end on the shoulder of a man. The rod makes an angle $\theta $ with the horizontal. Find the weight experienced by the man.
A) $W\cos \theta $
B) $W\sin \theta $
C) $W$
D) $\dfrac{W}{2}$

Answer 1

Hint: The heavy bar inclined at some angle with the ground is considered to be in mechanical equilibrium. Then the principle of moments suggests that the sum of the moments of the above system is zero. The net force acting on the given system will also be zero.

Formula used:
The moment of a force is given by, $d \times F = dF$ where $d$ is the perpendicular distance of the action of the force $F$.

Complete step by step answer:

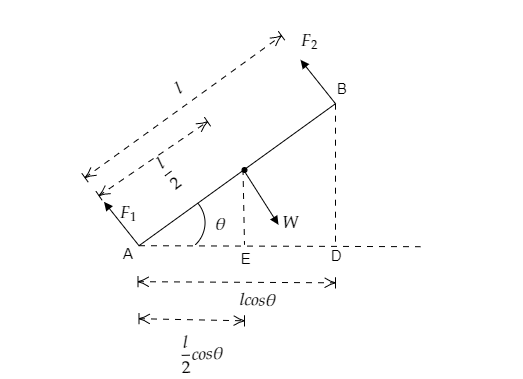
In the above figure, point A corresponds to the end of the bar on the ground and point B corresponds to the end of the bar on the shoulder of the man. AB represents the length of the bar $l$.
Here, the weight experienced by the man is the force ${F_2}$. The corresponding reaction on the ground is ${F_1}$.
Both ${F_1}$ and ${F_2}$ are directed upwards while the weight of the bar $W$ is directed downwards.
The net forces acting on the system can be expressed as ${F_1} + {F_2} = W$ .
The distance AE will be equal to $\dfrac{l}{2}\cos \theta $ and the distance AD represents the horizontal component of the length of the bar i.e., $l\cos \theta $.
Step 2: Use the principle of moments to find the weight experienced by the man.
Here, the weight of the bar $W$ tries to rotate the bar in the clockwise direction while the force ${F_2}$ tries to rotate the bar in the anticlockwise direction.
The principle fo moments gives the sum of the moments as zero.
i.e., ${F_2}\left( {AD} \right) - W\left( {AE} \right) = 0$
$ \Rightarrow {F_2}\left( {AD} \right) = W\left( {AE} \right)$ ------- (1)
Substituting for $AE = \dfrac{l}{2}\cos \theta $ and $AD = l\cos \theta $ in equation (1) we get, ${F_2}\left( {l\cos \theta } \right) = W\left( {\dfrac{l}{2}\cos \theta } \right)$
On simplifying the above expression we get, ${F_2} = \dfrac{W}{2}$

Thus the weight experienced by the man will be ${F_2} = \dfrac{W}{2}$. So the correct option is D.

Note:
The given system is said to be in mechanical equilibrium. This means that it is in a rotational as well as a translational equilibrium. The moment of a force refers to the torque acting. While writing the sum of the moments, the moment in the anticlockwise direction is taken as positive and the moment in the clockwise direction is taken as negative. The center of mass of the system is located in the middle of the bar.