Question

A heavy & big sphere is hang with a string of length l, this sphere moves in a horizontal circular path making an angle $\theta $ with vertical then its time period is:
A. \[T = 2\pi \sqrt {\dfrac{l}{g}} \]
B. $T = 2\pi \sqrt {\dfrac{{l\sin \theta }}{g}} $
C. $T = 2\pi \sqrt {\dfrac{{l\cos \theta }}{g}} $
D. $T = 2\pi \sqrt {\dfrac{l}{{g\cos \theta }}} $

Answer 1

Hint: By resolving the forces acting into horizontal and vertical components, we can calculate angular acceleration then time period can be calculated.

Complete step by step answer:
Let is consider a heavy big sphere of mass with a string length l as shown in the diagram below

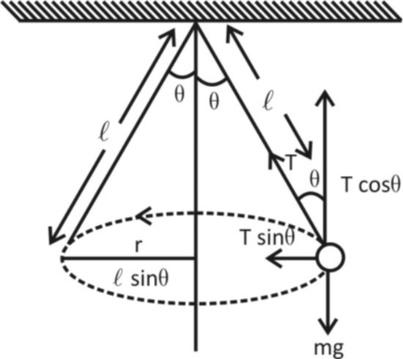
If the string makes angle $\theta $ with the vertical and T is the tension in the string. It can be resolved into two components.
(i) Tsin$\theta $ that provides the centripetal force
(ii) Tcos$\theta $ that balances the weight of sphere so, form figure it is clear that
Tcos$\theta = $mg … (i)
Tsin$\theta = $$\dfrac{{m{v^2}}}{r} = mr{\omega ^2}$
Where w is the angular acceleration and r is the radius of the horizontal circle.
Now, r$ = l\sin \theta $
So, Tsin$\theta = m\left( {l\sin \theta } \right){\omega ^2}$
$ \Rightarrow T = ml{\omega ^2}$… (ii)
Dividing (ii) by (i)
$\dfrac{T}{{T\cos \theta }} = \dfrac{{ml{\omega ^2}}}{{mg}}$
\[ \Rightarrow \dfrac{1}{{\cos \theta }} = \dfrac{{l{\omega ^2}}}{g} \Rightarrow {\omega ^2} = \dfrac{g}{{l\cos \theta }}\]
$ \Rightarrow \omega = \sqrt {\dfrac{g}{{l\cos \theta }}} $
As we know that w is related to time period as $\omega = \dfrac{{2\pi }}{T}$
So, $\dfrac{{2\pi }}{T} = \sqrt {\dfrac{g}{{l\cos \theta }}} $
$ \Rightarrow T = 2\pi \sqrt {\dfrac{{l\cos \theta }}{g}} $
Hence, time period is $2\pi \sqrt {\dfrac{{l\cos \theta }}{g}} $

So, the correct answer is “Option C”.

Note:
Remember that the bob is moving in a horizontal circle not in a vertical circle, so Tsin$\theta $ provides necessary centripetal force here. And the radius of the circle is r\[ = l\sin \theta \].