Question

A hawk sitting on a tree branch spots a mouse on the ground 15 feet from the base of the tree. The hawk swoops down toward the mouse at an angle of ${30^0}$. What is the distance from the tree branch to the mouse?
A. 7.5 ft
B. 15 ft
C. 26 ft
D. 30 ft

Answer 1

Hint:First draw the suitable diagram with careful visualization of the problem. Apply suitable trigonometry ratio formula having relationship between known and unknown terms and get the answer.

Complete step-by-step answer:
First, we draw the diagram for representation of the hawk and mouse and their relative positions.

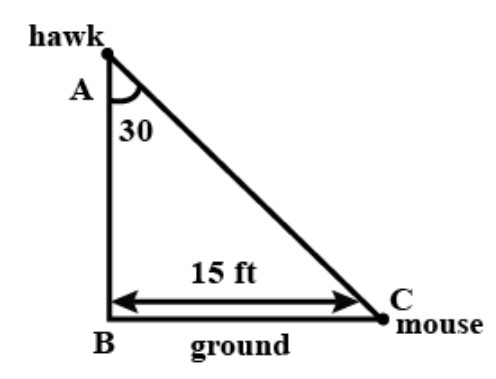
In triangle ABC, Hawk is at point A and mouse is at point C. From the diagram we can find the angle of depression from Hawk to mouse is ${30^0}$.
Given data in the problem is BC=15 ft. It is a horizontal distance.
Now, we know that sin of any angle is the ratio of perpendicular to the base in triangle.
Thus, we have
$\
  \sin {\theta} = \dfrac{{BC}}{{AB}} \\
    \\
 $
Substituting the values of sine and BC, we get
$\
  \sin {30^0} = \dfrac{{BC}}{{AB}} \\
   \Rightarrow \dfrac{1}{2} = \dfrac{{15}}{{AB}} \\
    \\
 $
Applying the transformation in above equation, we get,
AB = 30 ft
Thus, the distance from the tree branch to the mouse is 30 feet.

So, the correct answer is “Option D”.

Additional Information:In trigonometry, there are six trigonometric ratios. These are used to establish the relationship between sides and angle of the triangle. These are as follows:
Sine of the angle = $\dfrac{{Perpendicular}}{{Hypotenuse}}$
Cosine of the angle = $\dfrac{{Base}}{{Hypotenuse}}$
Tangent of the angle = $\dfrac{{Perpendicular}}{{Base}}$
Cosec of the angle = $\dfrac{{Hypotenuse}}{{Perpendicular}}$
Cotangent of the angle = $\dfrac{{Base}}{{Perpendicular}}$
Secant of the angle = $\dfrac{{Hypotenuse}}{{Base}}$
Based on the given values in the question, we may use relevant formulas. It is also clear that sin is the opposite ratio of cosec, cos is the opposite ratio of sec and tan is the opposite ratio of cot.

Note:Height and distance problems are the applications of trigonometry ratios and related formulas. Many complex geometrical problems can be solved with the help of trigonometry. Various derivations in science become easy with the proper use of trigonometry identities.