Question

A Hare sees a Dog 200 m away from her and scuds off in the opposite direction at a speed of 24 km/hr. Two minutes later the Dog perceives her and gives chase at a speed of 32 km/hr. How soon will the Dog overtake Hare and what is the distance from the spot from where the hare took flight?
A. 8 min, 2 km
B. $7\dfrac{1}{2}$ min , 2 km
C. $7\dfrac{1}{2}$ min, 3 km
D. $7\dfrac{1}{2}$ min, 1 km

Answer 1

Hint: In this question we are asked to find the distance and time taken by Dog to overtake Hare from where hare took flight. To find this first we need to elaborate the data given in the question with the help of a diagram. Then find the time taken by dog to overtake hare and the distance travel by hare with the help of formula $\text{Time=}\dfrac{\text{Distance}}{\text{Speed}}$ and $\text{Distance = time }\times \text{ speed}$ respectively.

Complete step-by-step answer:

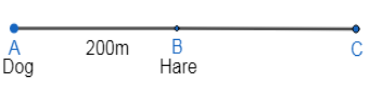
From the figure Let us consider that a Hare sees a Dog at point ‘A’ from point ‘B’ with a distance of 200m i.e. $AB=200m$ and scuds off in the opposite direction at a speed of 24 km/hr towards point ‘C’ where when the dog sees her after minutes,
$\therefore BC=$ the distance covered by the hare in 2 minutes.
Now, we will find the distance covered by hare in 2 minutes by taking the distance formula
i.e. $\text{Distance = time }\times \text{ speed}$
where, time = 2 minutes ; speed = 24 km / hr
So, $\text{Distance}=BC=24km/hr\times 2\min $
By taking $1km=1000m$ we will get –
$\begin{align}
  & =\dfrac{24\times 1000}{60}\times 2 \\
 & =\dfrac{24000}{30} \\
 & =800m \\
\end{align}$
$\therefore BC=800m$
Now, to overtake the hare, the dog has to travel a distance of $AC=AB+BC$. Where $AB=200m$ and $BC=800m$
So, $AC=\left( 800m+200m \right)=1000m$.
The relative speed of the dog can be calculated by subtracting speed of hare from the speed of dog
i.e. $32km/hr-24km/hr=8km/hr$.
Now, let us find the time taken by the dog to overtake hare –
We know that $\text{Time=}\dfrac{\text{Distance}}{\text{Speed}}$ , where, \[\text{Distance = 1000m = 1km}\] and $\text{Speed= 8km/hr}$ .
So, Time $=\dfrac{1}{8hr}=\left( \dfrac{1}{8}\times 60 \right)\min =7\dfrac{1}{2}$ .
Now, we will find the distance travelled by hare in $\dfrac{1}{8}hr$ is –
$\left( \dfrac{1}{8}\times 24 \right)km=3km$ $\left( \because \text{Distance = Time }\times \text{ Speed} \right)$.
Therefore, the distance travelled by hare in $\dfrac{1}{8}hr$ is 3km and time taken by the dog is $7\dfrac{1}{2}\min $ .
Hence, option (c) is the correct answer.

Note: Students might get confused while solving the problem as the data given in the question are in meters, kilometers, hour and minutes. They may make mistakes while calculating distance and time by taking $24km/hr\times 2\min $ in distance formula which may lead them to get the wrong answer. They should be very careful while calculating distance in meters and time in minutes.