Question

A hall can be paved with 200 square tiles of a certain size. If each tile were 5 cm longer each way it would take 128 tiles. Find the length of each tile.

Answer 1

Hint: Assume that the length of each side is x cm. In the \[{{1}^{st}}\] case, the hall is paved by 200 tiles. Now, get the area of one tile using the formula, \[{{\left( length\text{ }of\text{ }each\text{ }side\text{ }of\text{ }the\text{ }tile \right)}^{2}}\] . Calculate the area of 200 tiles. Since 200 tiles are required to pave the hall across the area, so the area of the hall is equal to the area of 200 tiles. Now, calculate the area in the \[{{1}^{st}}\] case. In the \[{{2}^{nd}}\] case, the hall is paved by 128 tiles. Now, get the area of one tile using the formula, \[{{\left( length\text{ }of\text{ }each\text{ }side\text{ }of\text{ }the\text{ }tile \right)}^{2}}\] . Calculate the area of 128 tiles. Since 128 tiles are required to pave the hall across the area, so the area of the hall is equal to the area of 128 tiles. Now, calculate the area in the \[{{2}^{nd}}\] case. Then, compare the area of the hall in the \[{{1}^{st}}\] case and the \[{{2}^{nd}}\] case. Solve it further and get the value of x.

Complete step-by-step answer:
According to the question, we have two cases.
Let us assume that the length of each side is x cm.
In the \[{{1}^{st}}\] case, we have to pave a hall with tiles. The number of tiles required to pave the hall is 200.

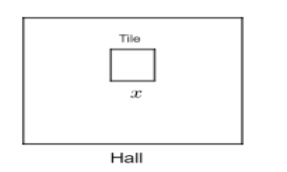
The length of each side of the tile = x cm ………………………………(1)
The total number of tiles required to pave the hall = 200 ………………………………………(2)
We know that the tiles are in the shape of the square. The area of the square is \[{{\left( side \right)}^{2}}\] . So, the area of tile is \[{{\left( length\text{ }of\text{ }each\text{ }side\text{ }of\text{ }the\text{ }tile \right)}^{2}}\] ……………………………….(3)
From equation (1), we have the length of each side of the tile.
From equation (1) and equation (3), we get
The area of each tile = \[{{x}^{2}}\,c{{m}^{2}}\] ………………………………….(4)
The area of 200 tiles = \[200{{x}^{2}}\,c{{m}^{2}}\] ……………………………………….(5)
Since 200 tiles are required to pave the hall across the area, so the area of the hall is equal to the area of 200 tiles.
From equation (5), we have the area of 200 tiles.
So, the area of the hall = \[200{{x}^{2}}\,c{{m}^{2}}\] ……………………………………….(6)
In the \[{{2}^{nd}}\] case, we have to pave a hall with tiles. The number of tiles required to pave the hall is 128. The length of each tile is increased by 5 cm.

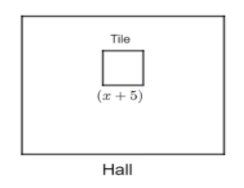
The length of each side of the tile = \[\left( x+5 \right)\] cm ………………………………(7)
The total number of tiles required to pave the hall = 128 ………………………………………(8)
We know that the tiles are in the shape of the square. The area of the square is \[{{\left( side \right)}^{2}}\] . So, the area of tile is \[{{\left( length\text{ }of\text{ }each\text{ }side\text{ }of\text{ }the\text{ }tile \right)}^{2}}\] ……………………………….(9)
From equation (7), we have the length of each side of the tile.
From equation (7) and equation (9), we get
The area of each tile = \[{{\left( x+5 \right)}^{2}}\,c{{m}^{2}}\] ………………………………….(10)
The area of 128 tiles = \[128{{\left( x+5 \right)}^{2}}\,c{{m}^{2}}\] ……………………………………….(11)
Since 128 tiles are required to pave the hall across the area, so the area of the hall is equal to the area of 128 tiles.
From equation (5), we have the area of 128 tiles.
So, the area of the hall = \[128{{\left( x+5 \right)}^{2}}\,c{{m}^{2}}\] ……………………………………….(12)
From equation (6) and equation (12), we have the area of the hall.
On comparing equation (6) and equation (12), we get
\[\begin{align}
  & \Rightarrow 200{{x}^{2}}\,c{{m}^{2}}=128{{\left( x+5 \right)}^{2}}\,c{{m}^{2}} \\
 & \Rightarrow 25{{x}^{2}}=16{{\left( x+5 \right)}^{2}} \\
 & \Rightarrow 25{{x}^{2}}=16{{x}^{2}}+160x+400 \\
 & \Rightarrow 25{{x}^{2}}-16{{x}^{2}}-160x-400=0 \\
 & \Rightarrow 9{{x}^{2}}-160x-400=0 \\
 & \Rightarrow 9{{x}^{2}}-180x+20x-400=0 \\
 & \Rightarrow 9x\left( x-20 \right)+20\left( x-20 \right)=0 \\
 & \Rightarrow \left( 9x+20 \right)\left( x-20 \right)=0 \\
\end{align}\]
So, \[x=\dfrac{-20}{9}\] or \[x=20\] .
The length of each side of the tile cannot be negative. So, \[x=\dfrac{-20}{9}\] is not possible.
The length of each side of the tile must be positive. So, \[x=20\] is possible.
Therefore, the length of each side of the tile is 20 cm.

Note:As the hall is paved by the tiles, one might get confused and think that the tile can be in the shape of a rectangle. As per the information provided in this question is that the tile is in the form of a square. So, we can use the formula of the area of a square to calculate the area of the tiles.