Question

A guy wire attached to a vertical pole of height 18 m is 24 m long and has a stake attached to the other end. How far from the base of the pole should the stake be driven so that the wire will be taut?
(a) 15.87 m
(b) 16.8 m
(c) 15 m
(d) 15.67 m

Answer 1

Hint: Assume height of the tower be ‘$h$’ m and the distance between the base of the pole and stake be $d$ m. Consider the length of wire as hypotenuse and use Pythagoras theorem in the right angle triangle formed to determine $d$.

Complete step-by-step solution -
It has been given to us that the height of the tower is 18 m and the total length of the wire is 24 m. We have assumed that the distance of the stake and base of the pole to keep the wire taut is ‘$d$’ m. The meaning of keeping the wire taut means that the wire should experience maximum tension at both ends and it should be kept in its full length and not loose.

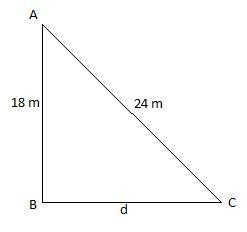
Now, when we will imagine how this system will look, we will observe that it looks like a right angle triangle in which wire is hypotenuse, height of pole is perpendicular and distance between stake and base of the pole as base of the triangle.
Therefore, applying Pythagoras theorem which is: $hypotenus{{e}^{2}}=bas{{e}^{2}}+perpendicula{{r}^{2}}$, we get,
$\begin{align}
  & {{24}^{2}}={{18}^{2}}+{{d}^{2}} \\
 & {{d}^{2}}={{24}^{2}}-{{18}^{2}} \\
 & \text{ =576-324} \\
 & \text{ =252} \\
 & \therefore \text{d=}\sqrt{252} \\
 & \text{ }=15.87 \\
\end{align}$
Hence, the distance between the base of pole and stake is 15.87 m.
Therefore, the correct option is (a).

Note: If the question would have said that the string is not taut, then we could not have applied Pythagoras theorem, as the system would not have been a right angle triangle. The wire length is taken as hypotenuse because it is opposite to the ${{90}^{\circ }}$ angle.