Question

A gulab jamun, contains sugar syrup up to about 30% of its volume. Find the approximately how much syrup would be found in 45 gulab jamuns each shaped like a cylinder with two hemispherical ends with length 5 cm and diameter 2.8 cm. \[\]

Answer 1

Hint: We find the volume of a single gulab jamun as the sum of the volume of the cylindrical part and volumes of the hemispherical part. We find the height of the cylinder $h$ and radius at the base $r$ from the given diameter and length of one gulab jamun and use the formula ${{V}_{c}}=\pi {{r}^{2}}h$. The radius at the base is same as radius of the hemisphere and volume of two hemisphere s at both ends is ${{V}_{h}}=2\times \dfrac{2}{3}\pi {{r}^{3}}=\pi {{r}^{2}}$. So the volume of one gulab jamun is ${{V}_{g}}={{V}_{c}}+{{V}_{h}}$ and syrups present in 45 gulab jamun is 30% of $45{{V}_{g}}$..\[\]

Complete step by step answer:
Let us consider one gulab jamun. We are given that the gulab jamun i shaped like a cylinder with two hemispherical ends with a length 5 cm and a diameter of 2.8 cm. Let us consider the following diagram\[\]
.

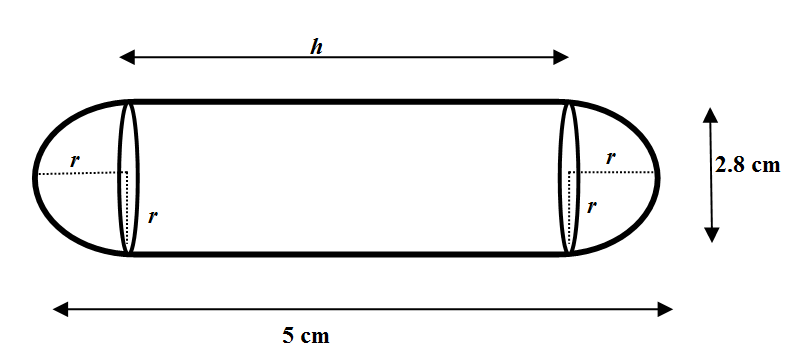
We see that the length of the gulab jamun is the sum of the height of the cylindrical part in the middle and the radii congruent hemispheres at the ends. The radius of the hemisphere is half of diameter, which is $r=\dfrac{2.8}{2}=1.4$cm. The length of the gulab jamun is $l=5$cm. So the height o the cylinder is
\[h=l-2r=5-2\times 1.4=2.2\text{ cm}\]
We see that the radius of any hemisphere is the radius of the base of the cylinder that is $r=1.4$cm. We use the formula $V=\pi {{r}^{2}}h$ and find the volume of the cylinder as,
\[\begin{align}
  & {{V}_{c}}=\pi {{r}^{2}}h \\
 & \Rightarrow {{V}_{c}}=\dfrac{22}{7}\times {{\left( 1.4 \right)}^{2}}\times 2.2 \\
 & \Rightarrow {{V}_{c}}=\dfrac{22}{7}\times 1.4\times 1.4\times 2.2 \\
 & \Rightarrow {{V}_{c}}=22\times 0.2\times 1.4\times 2.2 \\
 & \Rightarrow {{V}_{c}}=13.55\text{ c}{{\text{m}}^{3}} \\
\end{align}\]
We find the volume of one hemisphere with radius $r=1.4$cm as;
\[\begin{align}
  & {{V}_{h}}=\dfrac{2}{3}\times \pi {{r}^{3}} \\
 & \Rightarrow {{V}_{h}}=\dfrac{2}{3}\times \dfrac{22}{7}\times {{\left( 1.4 \right)}^{3}} \\
 & \Rightarrow {{V}_{h}}=\dfrac{2}{3}\times \dfrac{22}{7}\times 1.4\times 1.4\times 1.4 \\
 & \Rightarrow {{V}_{h}}=5.75\text{ c}{{\text{m}}^{3}} \\
\end{align}\]
The volume of one gulab jamun is sum of volumes of cylindrical part and the two congruent hemispheres which is
\[\begin{align}
  & {{V}_{g}}={{V}_{c}}+2{{V}_{h}} \\
 & \Rightarrow {{V}_{g}}=13.55+2\times 5.75 \\
 & \Rightarrow {{V}_{g}}=13.55+11.50 \\
 & \Rightarrow {{V}_{h}}=25.05\text{ c}{{\text{m}}^{3}} \\
\end{align}\]
Since we are given there are total 45 gulab jamuns, the total volume of gulab jamuns is
\[{{V}_{t}}=45\times {{V}_{g}}=45\times 25.05\text{ c}{{\text{m}}^{3}}\]
 We are also given a gulab jamun, containing sugar syrup up to about 30% of its volume. So the total amount of syrup from all gulab jamuns is 30% of ${{V}_{t}}$ which is
\[\text{Syrup in 45 gulab jamuns}=\dfrac{30}{100}\times {{V}_{t}}=\dfrac{30}{100}\times 25.05\times 45=338.175\text{ c}{{\text{m}}^{3}}\]

Note:
We note that we call hemispheres or spheres congruent when their radii are equal. We also note that drawing the diagram correctly is the key in the formula. We must not confuse in the formula for volume of hemisphere $V=\dfrac{2}{3}\pi {{r}^{3}}$ and the volume of a sphere $V=\dfrac{4}{3}\pi {{r}^{3}}$ and remember that the volume of a hemisphere s half of that of a sphere. We also note that when we say $p$% of $a$ it means $\dfrac{p}{100}\times a$ not $\dfrac{p}{a}\times 100$.