Question

A grassy field has the shape of an equilateral triangle of side $6$ m. A horse is tied to one of its vertices with a rope of length $4.2$ m. The percentage of the total area of the field which is available for grazing is best approximated by
A) $50\% $
B) $55\% $
C) $59\% $
D) $62\% $

Answer 1

Hint: An equilateral triangle is a triangle having all its sides equal. A horse tied to a point can graze on the land which can extend up to maximum of the length of the rope from the point of tying. We can say that a circle of radius equal to length of the rope is available for grazing for the horse.

Complete step-by-step solution:
We have a grassy field in the shape of an equilateral triangle. The sides of the triangle are $6$ m each.
So we can find the area of the field using the formula,
$A = \dfrac{{\sqrt 3 }}{4}{a^2}$
where, $a$ is the side of the triangle.
$A = \dfrac{{\sqrt 3 }}{4} \times {6^2} = \dfrac{{\sqrt 3 }}{4} \times 36 = 9\sqrt 3 $
Thus, the total area of the given field is $9\sqrt 3 $ m2.
Now, we are given that the horse is tied to one of the vertices with a rope of length $4.2$ m.
Thus, the horse can only graze on the portion of field which falls within its range of rope length, i.e. it can graze up to $4.2$ m only. This portion is shown in green in the diagram below.

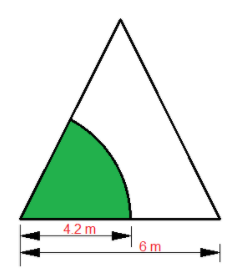
We have to calculate the area of the green portion which is the portion of the field which the horse can graze.
It is forming a sector of angle ${60^o}$ with radius $4.2$ m.
The area of a sector is given as,
\[
 \Rightarrow A = \dfrac{\theta }{{{{360}^o}}}\pi {r^2} \\
   \Rightarrow A = \dfrac{{{{60}^o}}}{{{{360}^o}}} \times \pi \times {(4.2)^2} \\
   \Rightarrow A = \dfrac{1}{6} \times 3.14 \times 17.64 \\
   \Rightarrow A = 9.23 \\
\]
Thus, the area within the field on which the horse can graze is $9.23$ m2.
Now, we have to calculate the percentage of the total area of the field which is available for grazing.
This can be calculated as follows,
% of field available for grazing = (Area of field available for grazing x 100) / (Total area of the field)
$
   \Rightarrow \dfrac{{9.23 \times 100}}{{9\sqrt 3 }}\% \\
   \Rightarrow \dfrac{{9.23 \times 100}}{{15.59}}\% \\
   \Rightarrow 59.20\% \\
$
Thus, the percentage of the total area of the field which is available for grazing is $59.20\% $, which can also be rounded as $59\% $.
Thus the correct answer is option ‘C’.
Note: Since the horse is tied to a vertex with rope length less than the side of the triangle, the horse cannot graze over the full field. Only a portion of a field is available for its grazing. This portion forms a sector with angle ${60^o}$ with radius $4.2$ m.