
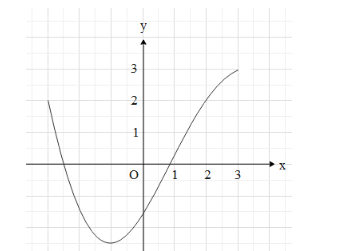
A graph of a function f is given. For what interval is f increasing?
A. (-1,3]
B. (-3,1)
C. (-3,1]
D. none of these

Answer
544.2k+ views
Hint: The function f is said to be increasing for a certain interval of x, if the value of y always increases with increase in the value of x belonging to that interval. Also, the slope of tangent to the curve at every point in these intervals is positive.
Complete step-by-step answer:
Let us first understand what is meant by increasing function.
A function is said to be increasing when the value of the function (dependent variable) increases when the value of the dependent variable increases.
Suppose we define a function
Also, when the function f is strictly increasing, its derivative with respect to x in that interval is always positive.
i.e.
Or we can also say that the slope of tangent to the curve at every point in these intervals is positive.
In the given graph, we can see that the function f is increasing for some interval of x and it's also decreasing for some interval of x.
With the above discussed points, we get that the function f is strictly increasing between
Therefore, the function f is increasing in the interval (-1,3].
So, the correct answer is “Option A”.
Note: Sometimes, students may make mistakes in using the correct brackets.
When we write the interval as (-1,3], it means that the value
Whereas the value
The tangent or derivative of the function at
Complete step-by-step answer:
Let us first understand what is meant by increasing function.
A function is said to be increasing when the value of the function (dependent variable) increases when the value of the dependent variable increases.
Suppose we define a function
Also, when the function f is strictly increasing, its derivative with respect to x in that interval is always positive.
i.e.
Or we can also say that the slope of tangent to the curve at every point in these intervals is positive.
In the given graph, we can see that the function f is increasing for some interval of x and it's also decreasing for some interval of x.
With the above discussed points, we get that the function f is strictly increasing between
Therefore, the function f is increasing in the interval (-1,3].
So, the correct answer is “Option A”.
Note: Sometimes, students may make mistakes in using the correct brackets.
When we write the interval as (-1,3], it means that the value
Whereas the value
The tangent or derivative of the function at
Recently Updated Pages
Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Trending doubts
Who composed the song Vande Mataram A RabindraNath class 10 social science CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE

The revolutionary who died after 63 days of the hunger class 10 social science CBSE

The slogan of Bande Mataram was first adopted during class 10 social science CBSE

Why is Sardar Vallabhbhai Patel called the Iron man class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE




