Question

A graph is plotted between ${\text{P(atm)}}$ vs ${{\text{t}}^{\text{o}}}{\text{C}}$ for ${\text{10mol}}$ of an ideal gas as follows:

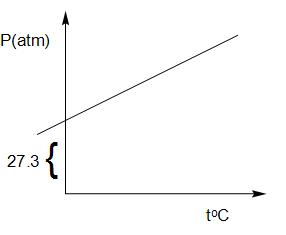
Then slope of curve and volume of container (L) respectively are:
A.$0.1,8.21$
B.$8.21,0.1$
C.$27.3,8.21$
D.$8.21,27.3$

Answer 1

Hint: To answer this question, you must recall the ideal gas law. The ideal gas equation gives an empirical relation among the volume, pressure, and number of moles and the temperature of an ideal gas.
Formula used:
$PV = nRT$
$P$ is the pressure of gas in atm
$V$ is the volume occupied by the gas (in liters)
$n$ is the number of moles of the gas
$T$ is the temperature in Kelvin
And, $R$ is the gas constant given by $R = 0.0821{\text{ atm L }}{{\text{K}}^{{\text{ - 1}}}}$

Complete step by step answer:
The graph represents a linear relation between the pressure and temperature of a gas. For a linear graph, the equation can be written as $y = mx + c$.
Where, $m$ is the slope of the graph
And, $c$ is the y- intercept
Thus, we can write, $P = mT + c$.
In the graph the intercept is given as $27.3$
So, the equation becomes $P = mT + 27.3$
We need to find the volume of the gas, so we consider the ideal gas equation at $T = 273{\text{K}}$
$PV = nRT$
Substituting the values, we get,
$27.3 \times V = 10 \times 0.0821 \times 273$
$ \Rightarrow V = 8.21{\text{ Litres}}$
Using the ideal gas equation for temperature in degree Celsius, $PV = nR\left( {T + 273} \right)$
$ \Rightarrow P = \dfrac{{nR}}{V}T + \dfrac{{nR}}{V} \times 273$
Substituting the values, we get,
$P = 0.1T + 27.3$
Comparing this equation with the equation of the graph, we get $m = 0.1$

Therefore, the correct answer is A.

Note:
The ideal gas equation is given for temperature in the unit Kelvin. Thus, care should be taken while substituting the value of temperature into the equation as the value of temperature in the question is given in the form of degree Celsius. A gas is considered to be ideal if:
The volume of the molecules of the gas is negligible as compared to the volume of the gas
There are no attractive forces present between the molecules of the gas.