
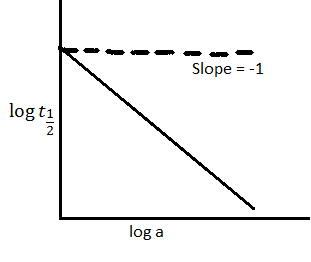
A graph between $\log {{t}_{1/2}}$ and log a (abscissa), 'a' is the initial concentration of A in the given reaction. For the reaction, $A\to \text{Product}$ , the rate law is:-
(A)$\dfrac{-d[A]}{dt}=K$
(B)$\dfrac{-d[A]}{dt}=K[A]$
(C)$\dfrac{-d[A]}{dt}=K{{[A]}^{2}}$
(D)$\dfrac{-d[A]}{dt}=K{{[A]}^{3}}$

Answer
533.1k+ views
Hint: The half-life of a reaction can be described as the amount of time required for a reactant concentration to decrease by half compared to its initial concentration. We will attempt this question by using the half time mathematical relation with initial concentration and convert it into a logarithmic equation as per the requirement of the graph and compare the values to get the desired answer.
Formula used:
The half-time relation with initial concentration is as follows:-
${{t}_{1/2}}=K{{a}^{1-n}}$
where,
n = order of the reaction.
K = rate constant
a = initial concentration of a substance.
${{t}_{1/2}}$ = half-life of the reaction
Complete step-by-step answer:
As we know that half-life is the time required for a quantity to reduce to half of its initial concentration. For any order of kinetics, the half-life relation with concentration is shown below:-
${{t}_{1/2}}=K{{a}^{1-n}}$
-Now we will convert this relation into logarithmic equation so as to compare it to the given graph:-
$\begin{align}
& \Rightarrow {{t}_{1/2}}=K{{a}^{1-n}} \\
& \text{On taking log both sides:} \\
& \Rightarrow \log {{t}_{1/2}}=\log (K{{a}^{1-n}}) \\
& \Rightarrow \log {{t}_{1/2}}=\log K+\log {{a}^{1-n}}\text{ (as log AB = log A+log B)} \\
& \Rightarrow \log {{t}_{1/2}}=\log K+(1-n)\log a\text{ (as log}{{\text{A}}^{x}}\text{ = xlogA)} \\
\end{align}$
-Since this is a straight line graph y = mx+c where m is the slope and c is the intercept. On comparing the above equation with straight line equation we get:-
Slope = (1-n)
Now let us take the help of given graph to determine the order of reaction:-
As it is given that slope = -1
Therefore, (1-n) = 1
And order of reaction (n) is = 2
-The rate law for a chemical reaction is an expression that provides the relationship between the concentration of the participating reactants and the rate of reaction.
For second order reaction, the rate law is: $\dfrac{-d[A]}{dt}=K{{[A]}^{2}}$
So, the correct answer is “Option C”.
Note:
The misunderstandings we have while solving kinetics questions are as follows:
(A)Order of a reaction is equal to the molecularity of the reaction. This is true but only for elementary reaction, not for complex reactions as molecularity is a positive integral value whereas order can be zero, negative, positive or fractional.
(B)We should not forget to consider stoichiometry while writing or using the rate expression or our obtained results will be wrong.
Formula used:
The half-time relation with initial concentration is as follows:-
${{t}_{1/2}}=K{{a}^{1-n}}$
where,
n = order of the reaction.
K = rate constant
a = initial concentration of a substance.
${{t}_{1/2}}$ = half-life of the reaction
Complete step-by-step answer:
As we know that half-life is the time required for a quantity to reduce to half of its initial concentration. For any order of kinetics, the half-life relation with concentration is shown below:-
${{t}_{1/2}}=K{{a}^{1-n}}$
-Now we will convert this relation into logarithmic equation so as to compare it to the given graph:-
$\begin{align}
& \Rightarrow {{t}_{1/2}}=K{{a}^{1-n}} \\
& \text{On taking log both sides:} \\
& \Rightarrow \log {{t}_{1/2}}=\log (K{{a}^{1-n}}) \\
& \Rightarrow \log {{t}_{1/2}}=\log K+\log {{a}^{1-n}}\text{ (as log AB = log A+log B)} \\
& \Rightarrow \log {{t}_{1/2}}=\log K+(1-n)\log a\text{ (as log}{{\text{A}}^{x}}\text{ = xlogA)} \\
\end{align}$
-Since this is a straight line graph y = mx+c where m is the slope and c is the intercept. On comparing the above equation with straight line equation we get:-
Slope = (1-n)
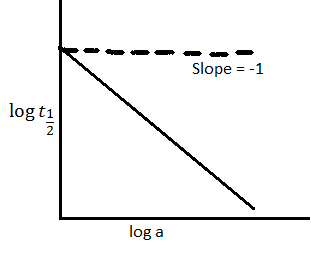
Now let us take the help of given graph to determine the order of reaction:-

As it is given that slope = -1
Therefore, (1-n) = 1
And order of reaction (n) is = 2
-The rate law for a chemical reaction is an expression that provides the relationship between the concentration of the participating reactants and the rate of reaction.
For second order reaction, the rate law is: $\dfrac{-d[A]}{dt}=K{{[A]}^{2}}$
So, the correct answer is “Option C”.
Note:
The misunderstandings we have while solving kinetics questions are as follows:
(A)Order of a reaction is equal to the molecularity of the reaction. This is true but only for elementary reaction, not for complex reactions as molecularity is a positive integral value whereas order can be zero, negative, positive or fractional.
(B)We should not forget to consider stoichiometry while writing or using the rate expression or our obtained results will be wrong.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




