
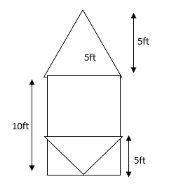
A grain silo is built from two right circular cones and a right circular cylinder with internal measurements represented by the figure above, On the following which is closest to the volume of grain silo, in cubic feet?
(A)$261.8$
(B) $785.4$
(C)$916.3$
(D)$1,047.2$

Answer
583.8k+ views
Hint: According to the figure- There are two cones and one cylinder and we have to find grain kilo volume.Therefore, Total volume of grain silo= Volume of cylinder+2(Volume of cone)
Complete step-by-step answer:
In the question a figure is given so we could solve it by using the figure.
As given in the figure: - height of cone$ = 5ft.$
Height of cylinder$ = 10ft$
Radius of cone and also cylinder$ = 5ft.$
According to the figure- There are two cones and one cylinder and we have to find grain kilo volume.
Therefore, Total volume of grain silo= Volume of cylinder+2(Volume of cone)
Now we use that formula
Volume of cone$ = \pi {r^2}h.$
Volume of cone$ = \dfrac{1}{3}\pi {r^2}h.$
Here,$h = height$$r = radius.$
Now by putting the formula
Total volume of grain silo= Volume of cylinder + 2 (Volume of cones)
Volume of grain silo=$\pi {r^2} + 2\left( {\dfrac{1}{3}\pi {r^2}h} \right).$
$ \Rightarrow $From the figure put the value of$n$and$r.$
$ = \pi \times {(5)^2} \times 10 + 2\left( {\dfrac{1}{3} \times \pi \times {{(5)}^2} \times 5} \right)$
Taking$\pi $common.
$ = \pi \left[ {25 \times 10 + \dfrac{{2 \times 125}}{3}} \right]$
$ = \pi \left[ {\dfrac{{250 \times 3 + 250}}{3}} \right]$
$ = \pi \left[ {\dfrac{{750 + 250}}{3}} \right]$
$ = \pi \left[ {\dfrac{{1000}}{3}} \right]$
$ = \dfrac{{22}}{7}\left[ {\dfrac{{1000}}{3}} \right]$
$ = 1047.2$
So, the correct answer is “Option D”.
Note: We use the following formula to find the total volume of the grain as the figure consist of 2 cones and a cylinder Volume of cone$ = \pi {r^2}h.$
Volume of cone$ = \dfrac{1}{3}\pi {r^2}h.$
Complete step-by-step answer:
In the question a figure is given so we could solve it by using the figure.

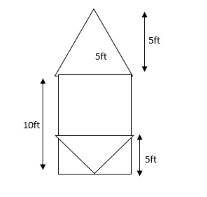
As given in the figure: - height of cone$ = 5ft.$
Height of cylinder$ = 10ft$
Radius of cone and also cylinder$ = 5ft.$
According to the figure- There are two cones and one cylinder and we have to find grain kilo volume.
Therefore, Total volume of grain silo= Volume of cylinder+2(Volume of cone)
Now we use that formula
Volume of cone$ = \pi {r^2}h.$
Volume of cone$ = \dfrac{1}{3}\pi {r^2}h.$
Here,$h = height$$r = radius.$
Now by putting the formula
Total volume of grain silo= Volume of cylinder + 2 (Volume of cones)
Volume of grain silo=$\pi {r^2} + 2\left( {\dfrac{1}{3}\pi {r^2}h} \right).$
$ \Rightarrow $From the figure put the value of$n$and$r.$
$ = \pi \times {(5)^2} \times 10 + 2\left( {\dfrac{1}{3} \times \pi \times {{(5)}^2} \times 5} \right)$
Taking$\pi $common.
$ = \pi \left[ {25 \times 10 + \dfrac{{2 \times 125}}{3}} \right]$
$ = \pi \left[ {\dfrac{{250 \times 3 + 250}}{3}} \right]$
$ = \pi \left[ {\dfrac{{750 + 250}}{3}} \right]$
$ = \pi \left[ {\dfrac{{1000}}{3}} \right]$
$ = \dfrac{{22}}{7}\left[ {\dfrac{{1000}}{3}} \right]$
$ = 1047.2$
So, the correct answer is “Option D”.
Note: We use the following formula to find the total volume of the grain as the figure consist of 2 cones and a cylinder Volume of cone$ = \pi {r^2}h.$
Volume of cone$ = \dfrac{1}{3}\pi {r^2}h.$
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Difference Between Plant Cell and Animal Cell

Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Who is eligible for RTE class 9 social science CBSE

Which places in India experience sunrise first and class 9 social science CBSE

What is pollution? How many types of pollution? Define it

Name 10 Living and Non living things class 9 biology CBSE




