Question

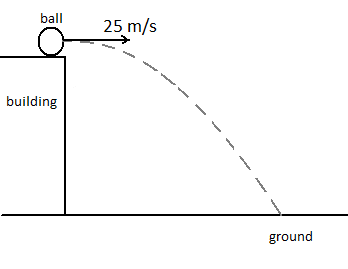
A golf ball is hit off the roof of a building into an open lot next to the building. The ball is hit so that it launches straight horizontally from the roof, at the launch speed of 25 ms-1. If the golf ball lands on the ground 4 seconds after it was hit, how far away from the building (measured horizontally) does it land?
(A) $6.25\,{\text{meters}}$
(B) $100\,{\text{meters}}$
(C)$180\,{\text{meters}}$
(D) This question cannot be answered without knowing the height of the building

Answer 1

Hint: Distance of building from which the golf ball land is found using the distance and speed relation formula. Substitute the values of speed of the ball and the time taken to travel in the formula to obtain the distance travelled by the ball.

Useful formula:
According to the speed and distance relationship,
${\text{Distance = }}s \times t$
Where, $s$ is the speed at which the ball travels and $t$ is the time taken by the ball to hit the wall and fall down.

Complete step by step solution:
Given data from the question are
Speed at which the ball travels, $s = 25\,m{s^{ - 1}}$
Time taken by the ball to travel, $t = 4\,s$
Hence according to the above formula, distance travelled by the ball is given by

$D = s \times t$
Substituting the above values in the formula,
$D = 25 \times 4$
$D = 100\,m$
Distance that the ball lands from the building is $100\,m$.

Thus, the option (B) is correct.

Additional information: Speed is defined as the rate of change of the position of the object with respect to the time. Distance is directly proportional to speed. Speed is a scalar quantity. Its unit is $m{s^{ - 1}}$.But time and speed are inversely proportional to each other. As speed increases, time taken to reach the particular distance decreases.

Note: Speed and distance relationship must be noted carefully, because the product of speed and time only gives the answer for distance travelled. Remembering the formula and simple substitution of the values in it is enough to solve this problem.