Question

A goalkeeper in a game of football pulls his hands backward while holding the ball shot at the goal. This enables the goalkeeper to
A) exert large on the ball.
B) reduce the force by the ball on hands.
C) increase the rate of change of momentum of the ball.
D) decrease the rate of change of momentum of the ball.

Answer 1

Hint:As the ball comes towards the keeper with a high speed, it will have large momentum because:
Momentum (p) = Mass (m) $\times$ Velocity (v)
We can provide the reason in the same context. Also,
According to Newton’s second law of motion,
Force is directly proportional to the rate of change of linear (in a straight line) momentum.
$F \propto \dfrac{{dp}}{{dt}}$

Complete step by step answer:

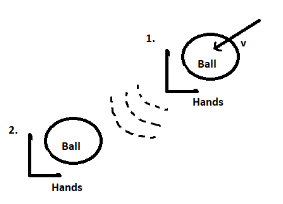
When the ball comes towards the keeper, it has greater speed (as it is coming fast).
As momentum is the product of mass and velocity (p = mv), the momentum of this ball is large.
i) If the hands will be at rest in position 1. In the diagram, the velocity will be 0:
p = mv ; p = 0 if v=0
The hands will have no momentum, so when the ball will come towards them, the rate of change of momentum (between the ball and hands) will be large and a large force will be exerted on hands because:
$F \propto \dfrac{{dp}}{{dt}}$
So, when the rate of change of momentum is large, the force will also be large
ii) If the hands are moved backward from position 1. To position 2. The momentum of the hand increases as some velocity is provided.
Now, when the ball will come towards them, the rate of change of momentum (between the ball and hands) will be small and a lesser force will be exerted on hands because:
$F \propto \dfrac{{dp}}{{dt}}$
So, when the rate of change of momentum is small, the force will also be lesser.
It can be seen that the goalkeeper pulls his hands backward while holding the ball shot at the goal to reduce the rate of change of momentum which in turn reduces the force exerted on the hands by the ball.
Thus, the correct options are both B) and D).

Note: We have two types of proportionalities, direct and inverse:
$a \propto b$ a is directly proportional to b; with the increase in a, b also increases.
$a \propto \dfrac{1}{b}$ a is inversely proportional to b; with the increase in a, b decreases.
If any quantity A is written as:
$\dfrac{{dA}}{{dt}}$; it shows the rate of change of momentum of A.
Newton’s second law of motion can also be interpreted as:
$F \propto \dfrac{{dp}}{{dt}} \to F = K\dfrac{{dp}}{{dt}}$ K is any proportionality constant which can be neglected.
Substituting the value of p:
$
F = \dfrac{{dp}}{{dt}} \\
\Rightarrow F = \dfrac{{d(mv)}}{{dt}} \\
$
Now, mass is constant and the rate of change of velocity is acceleration.
So, the expression becomes:F = ma