Question

A glass dumbbell of length \[30{\rm{ cm}}\] and \[\mu = 1.5\] has ends \[3{\rm{ cm}}\] radius of curvature. An object is situated in air at a distance of \[12{\rm{ cm}}\] from the end of dumb-bell along the axis. The position of image formed due to refraction at one end only is
A. \[16{\rm{ cm}}\]
B. \[18{\rm{ cm}}\]
C. \[20{\rm{ cm}}\]
D. \[24{\rm{ cm}}\]

Answer 1

Hint: We will be using the relation between image distance from the glass and the object distance from the glass, this relation is also contains two refractive index out of which one is for the medium from which light is coming and the other is for the medium in which image is being formed.

Complete step by step answer:
Given:
The length of the dumb-bell is \[L = 30{\rm{ cm}}\].
Refractive index of dumb-bell glass is \[\mu = 1.5\].
Radius of curvature of the dumb-bell ends is \[R = 3{\rm{ cm}}\].
Object distance from the end of dumb-bell is \[u = 12{\rm{ cm}}\].
Image distance from the end of the dumb-bell is v.

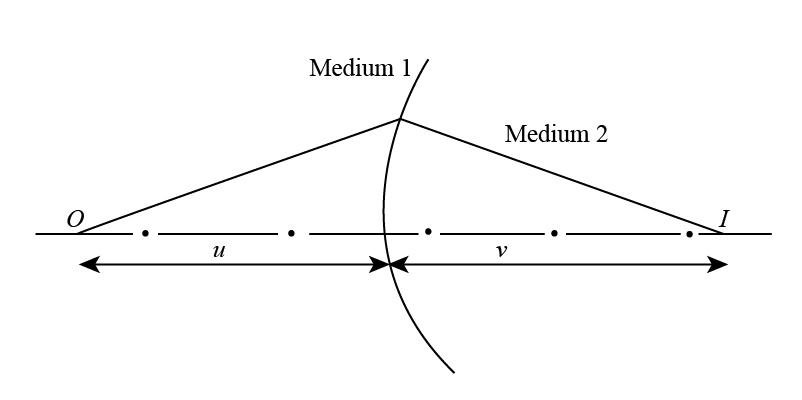
Relation for image distance, object distance, radius of curvature and refractive indexes of the mediums is given as:
\[\dfrac{\mu }{v} - \dfrac{{\mu '}}{u} = \dfrac{{\mu - \mu '}}{R}\]……(1)

The object is placed in open so the refracting index of the environment is taken for \[\mu '\] whose value is unity.

Taking sign convention and substituting \[ - 12{\rm{ cm}}\] for u, \[3{\rm{ cm}}\] for R, \[1\] for \[\mu '\] and \[1.5\] for \[\mu \] in equation (1).
\[\begin{array}{c}
\dfrac{{1.5}}{v} - \dfrac{1}{{\left( { - 12{\rm{ cm}}} \right)}} = \dfrac{{1.5 - 1}}{{3{\rm{ cm}}}}\\
\dfrac{{1.5}}{v} = \dfrac{1}{{6{\rm{ cm}}}} - \dfrac{1}{{12{\rm{ cm}}}}\\
v = 18{\rm{ cm}}
\end{array}\]

Therefore, the image formed at a distance of \[18{\rm{ cm}}\] due to the refraction on one endV

So, the correct answer is “Option B”.

Note:
Take care of the sign convention as the image has to be formed of the other side of the glass due to refraction.