Question

A given right circular cone has a volume p and the largest right circular cylinder that can be inscribed in the cone has a volume q. Then p : q is
(a) 9 : 4
(b) 8 : 3
(c) 7 : 2
(d) None of these

Answer 1

Hint: Consider r, h and R, H as the radius of cone and cylinder. Find relation between r, h, R and H. Take angle as \[\theta \]. Now consider the volume of the cylinder, \[V=\pi {{R}^{2}}h\] and differentiate it twice and get a relation between H and h. Now find volume of cylinder q, volume of cone p and take their ratio.

Complete step-by-step answer:
It is said that the largest right circular cylinder is inscribed inside the right circular cone. Consider the figure drawn. Let AFG be the right circular cone and BCED be the right circular cylinder.

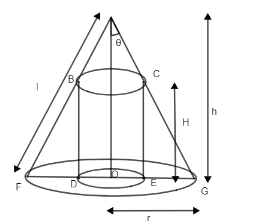
Let r and h be the radius and height of the right circular cone. Similarly let R and H be the radius and height of the right circular cylinder.
Let us consider \[\angle GAO=\theta \],
From the figure OG = r, OE = R, OA = h and CE = H.
We can say that from \[\Delta AOG\] in the figure,
\[\tan \theta \] = opposite side / adjacent side = \[\dfrac{OG}{OA}=\dfrac{r}{h}\]
\[\therefore r=h\tan \theta \] - (1)
From the figure we can say that \[\Delta AOG\] and \[\Delta CEG\] are similar triangles. Thus we can say that their sides are proportional.
\[\dfrac{AO}{OG}=\dfrac{CE}{EG}\]
Put AO = h, OG = r, CE = H, EG = OG – OE = r –R [from figure]
\[\begin{align}
  & \therefore \dfrac{h}{r}=\dfrac{H}{EG} \\
 & \dfrac{h}{r}=\dfrac{H}{r-R} \\
\end{align}\]
\[\Rightarrow H=\dfrac{h}{r}\left( r-R \right)\] - (2)
Put the value of (1) in (2). Hence, we get,
\[\begin{align}
  & H=\dfrac{h}{r}\left( r-R \right) \\
 & H=\dfrac{h}{h\tan \theta }\left( h\tan \theta -R \right)=\dfrac{h\tan \theta -R}{\tan \theta } \\
\end{align}\]
We know that volume of cylinder = \[\pi {{R}^{2}}H\], put \[H=\dfrac{h\tan \theta -R}{\tan \theta }\], in the formula to find volume of cylinder.
\[\begin{align}
  & \therefore V=\dfrac{\pi {{R}^{2}}\left( h\tan \theta -R \right)}{\tan \theta } \\
 & V=\dfrac{\pi {{R}^{2}}h\tan \theta }{\tan \theta }-\dfrac{\pi {{R}^{3}}}{\tan \theta }=\pi {{R}^{2}}h-\dfrac{\pi {{R}^{3}}}{\tan \theta } \\
\end{align}\]
\[V=\pi {{R}^{2}}h-\dfrac{\pi {{R}^{3}}}{\tan \theta }\] - (3)
Let us find the derivative of the above function,
\[\dfrac{dV}{dR}=\dfrac{d}{dR}\left[ \pi {{R}^{2}}h-\dfrac{\pi {{R}^{3}}}{\tan \theta } \right]\]
\[\dfrac{dV}{dR}=2\pi Rh-\dfrac{3\pi {{R}^{2}}}{\tan \theta }\] - (4)
Put, \[\dfrac{dV}{dR}=0\].
\[\begin{align}
  & \Rightarrow 2\pi Rh-\dfrac{3\pi {{R}^{2}}}{\tan \theta }=0 \\
 & \therefore 2\pi Rh=\dfrac{3\pi {{R}^{2}}}{\tan \theta } \\
\end{align}\]
Cancel out the like terms.
\[R=\dfrac{2h}{3}\tan \theta \] - (5)
Let us take the second derivative of (4).
\[\dfrac{d{{V}^{2}}}{d{{R}^{2}}}=\dfrac{d}{dR}\left[ 2\pi Rh-\dfrac{3\pi {{R}^{2}}}{\tan \theta } \right]\]
\[\dfrac{d{{V}^{2}}}{d{{R}^{2}}}=2\pi h-\dfrac{6\pi R}{\tan \theta }\] - (6)
Let us substitute the value of R in the above expression (6).
\[\dfrac{d{{V}^{2}}}{d{{R}^{2}}}=2\pi h-\left[ \dfrac{6\pi }{\tan \theta }\times \dfrac{2h}{3}\tan \theta \right]=2\pi h-4\pi h=-2\pi h<0\]
Thus by the second derivative test the volume of the cylinder is maximum when, \[R=\dfrac{2h}{3}\tan \theta \].
Thus in (2) put value of \[R=\dfrac{2h}{3}\tan \theta \] and \[r=h\tan \theta \].
\[\begin{align}
  & \therefore H=\dfrac{h}{r}\left( r-R \right)=\dfrac{h}{h\tan \theta }\left[ h\tan \theta -\dfrac{2h}{3}\tan \theta \right] \\
 & \therefore H=\dfrac{h}{r}\left( r-R \right)=\dfrac{h\tan \theta }{h}\left[ 1-\dfrac{2}{3} \right]=\dfrac{h}{3} \\
\end{align}\]
Thus we get, \[H=\dfrac{h}{3}\].
Hence the height of the cylinder is one third the height of the cone. The maximum volume of the cylinder is,
\[\begin{align}
  & q=\pi {{R}^{2}}H=\pi {{\left[ \dfrac{2h}{3}\tan \theta \right]}^{2}}\times \dfrac{h}{3} \\
 & q=\pi \dfrac{4{{h}^{2}}}{9}{{\tan }^{2}}\theta \times \dfrac{h}{3}=\dfrac{4\pi {{h}^{3}}}{27}{{\tan }^{2}}\theta \\
\end{align}\]
The volume of the cone = p = \[\dfrac{1}{3}\pi {{r}^{2}}h\]
\[\begin{align}
  & p=\dfrac{1}{3}\pi {{\left( h\tan \theta \right)}^{2}}h \\
 & p=\dfrac{1}{3}\pi {{h}^{3}}{{\tan }^{2}}\theta \\
\end{align}\]
Hence the required ratio = \[\dfrac{p}{q}\] = volume of cone / volume of cylinder
\[\therefore \dfrac{p}{q}=\dfrac{\dfrac{1}{3}\pi {{h}^{3}}{{\tan }^{2}}\theta }{\dfrac{4}{27}\pi {{h}^{3}}{{\tan }^{2}}\theta }=\dfrac{1}{3}\times \dfrac{27}{4}=\dfrac{9}{4}\]
Thus we got the required ratio of p : q as 9 : 4.
\[\therefore \] Option (a) is the correct answer.

Note: As the right circular cylinder is inscribed inside the cone it is important that you find relations connecting to the radius and height of both cylinder and cone. The ultimate relation we have to get is \[H=\dfrac{h}{3}\].