Question

A given quantity of metal is to be cast into a solid half-circular cylinder (i.e. with a rectangular base and semicircular ends) Show that in order that the total surface area may be minimum, the ratio of the length of the cylinder to the diameter of the circular ends is $\dfrac{\pi }{\pi +2}$ .

Answer 1

Hint: To find the extrema we need to find the first differentiation and equate it to zero. The condition is written as follows, $\dfrac{dS}{dr}=0$ . And to check which it’s minima and maxima the condition is $\dfrac{{{d}^{2}}S}{d{{r}^{2}}}>0$ , then it’s a minima and when $\dfrac{{{d}^{2}}S}{d{{r}^{2}}}<0$ then it’s a maxima.

Complete step by step answer:
We need to minimize the surface area of the half-cylinder.
The half-cylinder is the cylinder chopped in half such that there is a rectangular base and semicircular ends.
It can be shown in figures are below,

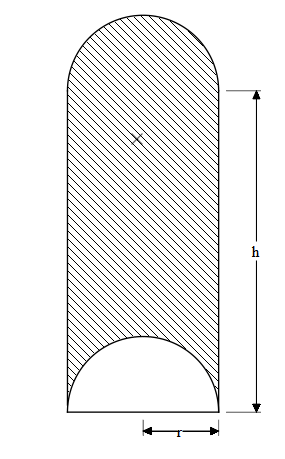
Let this be the half-cylinder with radius $r$ and height $h$ .
This half cylinder is exactly half of the original cylinder so the volume of the cylinder will be also halved.
Therefore, the volume of the half-cylinder $V=\dfrac{1}{2}\times \pi {{r}^{2}}h$ .
We will find the expression of $h$ in terms if V we get,
$\Rightarrow h=\dfrac{2V}{\pi {{r}^{2}}}..............(i)$
Now, let's find the surface area of this half-cylinder,
There is a rectangular base, two half circles and a curved surface.
Therefore, Total surface area (S) = area of rectangle + area of 2 semi-circles + area of the curved surface,
By looking at the figure, we can see that,
$S=h\times 2r+2\times \dfrac{1}{2}\pi {{r}^{2}}+\dfrac{1}{2}\times 2\pi rh$ .
Simplifying it further, we get,
$S=2rh+\pi {{r}^{2}}+\pi h..................(ii)$
 From equation (i) let's substitute the value of $h$ ,
By substituting we get,
$S=2r\times \left( \dfrac{2V}{\pi {{r}^{2}}} \right)+\pi {{r}^{2}}+\pi r\left( \dfrac{2V}{\pi {{r}^{2}}} \right)..........................(iii)$
In order to find the extrema, we need to find the first differentiation and equate it to zero.
Therefore, $\dfrac{dS}{dr}=0$ .
Solving we get,
$\dfrac{dS}{dr}=\dfrac{-4V}{\pi {{r}^{2}}}+2\pi r-\dfrac{2V}{{{r}^{2}}}=0$
Solving for the value of $r$ , we get,
$\begin{align}
  & 2\pi r=\dfrac{2V}{{{r}^{2}}}+\dfrac{4V}{\pi {{r}^{2}}} \\
 & \Rightarrow {{r}^{3}}=\dfrac{V}{\pi }+\dfrac{2V}{{{\pi }^{2}}}.................(iv) \\
\end{align}$
To find whether it’s maxima or minima we need to differentiate again. If $\dfrac{{{d}^{2}}S}{d{{r}^{2}}}>0$ then it’s a minima and if $\dfrac{{{d}^{2}}S}{d{{r}^{2}}}<0$ it’s a maxima.
Therefore, $\dfrac{{{d}^{2}}S}{d{{r}^{2}}}=2\pi +\dfrac{1}{{{r}^{3}}}\left( \dfrac{4V}{\pi }+2V \right)$ . As all the numbers are positive $\dfrac{{{d}^{2}}S}{d{{r}^{2}}}>0$,
Therefore, it’s minima.
Now we need to eliminate the V from equation (iv) and (i),
From (iv) we get,
$\begin{align}
  & \Rightarrow {{r}^{3}}=V\left( \dfrac{1}{\pi }+\dfrac{2}{{{\pi }^{2}}} \right) \\
 & \Rightarrow V=\dfrac{{{r}^{3}}}{\left( \dfrac{1}{\pi }+\dfrac{2}{{{\pi }^{2}}} \right)}..................(v) \\
\end{align}$
Substituting in equation (i) we get,
$\dfrac{{{r}^{3}}}{\left( \dfrac{1}{\pi }+\dfrac{2}{{{\pi }^{2}}} \right)}=\dfrac{1}{2}\times \pi {{r}^{2}}h$
Solving for $\dfrac{2r}{h}$ , we get,
$\begin{align}
  & \dfrac{2r}{h}=\pi \left( \dfrac{1}{\pi }+\dfrac{2}{{{\pi }^{2}}} \right) \\
 & \Rightarrow \dfrac{2r}{h}=1+\dfrac{2}{\pi } \\
 & \Rightarrow \dfrac{2r}{h}=\dfrac{\pi +2}{\pi } \\
\end{align}$
Taking the inverse, we get,
$\dfrac{h}{2r}=\dfrac{\pi }{\pi +2}$
Hence, the ratio of the length of the cylinder to diameter is $\dfrac{\pi }{\pi +2}$ .

Note: We need to calculate the surface area carefully because there are chances that anyone semicircle can be easily missed out. Also, we need to find the ratio of the length to the diameter and not the radius so we need to consider $2r$ instead of $r$ . While differentiation we need to also check the double differentiation and if it is greater than zero then the extrema is minima.