Question

A given quantity of metal is to be cast into a half cylinder with a rectangular base and semi-circular ends. Show that in order that the total surface area may be minimum, the ratio of the length of the cylinder to the diameter of its semi-circular ends is $\pi :\left( {\pi + 2} \right)$.

Answer 1

Hint- Here, we will proceed by finding the total surface area of the given half cylinder and then we will convert this surface area in terms of radius of the semi-circular ends alone. Then, we will differentiate it and equate this equal to zero.

To show: Ratio of the length of the cylinder to the diameter of its semi-circular ends is $\pi :\left( {\pi + 2} \right)$ or $\dfrac{{{\text{Length of the cylinder}}}}{{{\text{Diameter of its semi - circular ends}}}} = \dfrac{\pi }{{\pi + 2}}$

Complete step by step answer:
So, we have to prove the above equation
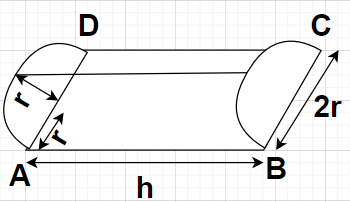
Let us consider a cylinder of length (or height) h having a rectangular base and semi-circular ends of radius r as shown in the figure.
As we know that the formula for the area of the semicircle with radius r is given by
Area of the semicircle = $\dfrac{{\pi {r^2}}}{2}$
Also, the curved surface area of half cylinder having radius r and length h is given by
Curved surface area of half cylinder = $\pi rh$
Also, the area of any rectangle is given by
Area of the rectangle = (Length of the rectangle)$ \times $(Breadth of the rectangle)
Using the above formula, we can write
Area of the rectangular base ABCD = (AB) $ \times $(BC) = h$ \times $2r = 2rh
Total surface area of the half cylinder = Area of two semi-circular ends + Curved surface area of half cylinder + Area of the rectangular base ABCD
$ \Rightarrow $ TSA = $2\left( {\dfrac{{\pi {r^2}}}{2}} \right) + \pi rh + 2rh$
$ \Rightarrow $ TSA = $\pi {r^2} + \pi rh + 2rh$
$ \Rightarrow $ TSA = $\pi {r^2} + \left( {\pi + 2} \right)rh{\text{ }} \to {\text{(1)}}$
As we know that volume of the half cylinder having radius as r and length as h is given by
$
  {\text{V}} = \dfrac{{\pi {r^2}h}}{2} \\
   \Rightarrow h = \dfrac{{2{\text{V}}}}{{\pi {r^2}}}{\text{ }} \to {\text{(2)}} \\
 $
By substituting equation (2) in equation (1), we get
$ \Rightarrow $ TSA = $\pi {r^2} + \left( {\pi + 2} \right)r\left( {\dfrac{{2{\text{V}}}}{{\pi {r^2}}}} \right)$
$ \Rightarrow $ TSA = $\pi {r^2} + \left( {\pi + 2} \right)\left( {\dfrac{{2{\text{V}}}}{{\pi r}}} \right)$
By differentiating the above equation on both sides with respect to r, we get
\[
   \Rightarrow \dfrac{d}{{dr}}\left( {{\text{TSA}}} \right) = \dfrac{d}{{dr}}\left[ {\pi {r^2} + \left( {\pi + 2} \right)\left( {\dfrac{{2{\text{V}}}}{{\pi r}}} \right)} \right] \\
   \Rightarrow \dfrac{d}{{dr}}\left( {{\text{TSA}}} \right) = \dfrac{d}{{dr}}\left( {\pi {r^2}} \right) + \dfrac{d}{{dr}}\left[ {\left( {\pi + 2} \right)\left( {\dfrac{{2{\text{V}}}}{{\pi r}}} \right)} \right] \\
   \Rightarrow \dfrac{d}{{dr}}\left( {{\text{TSA}}} \right) = \pi \dfrac{d}{{dr}}\left( {{r^2}} \right) + \left( {\pi + 2} \right)\left( {\dfrac{{2{\text{V}}}}{\pi }} \right)\dfrac{d}{{dr}}\left( {{r^{ - 1}}} \right) \\
   \Rightarrow \dfrac{d}{{dr}}\left( {{\text{TSA}}} \right) = \pi \left( {2r} \right) + \left( {\pi + 2} \right)\left( {\dfrac{{2{\text{V}}}}{\pi }} \right)\left( { - {r^{ - 2}}} \right) \\
   \Rightarrow \dfrac{d}{{dr}}\left( {{\text{TSA}}} \right) = 2\pi r + \left( {\pi + 2} \right)\left( {\dfrac{{2{\text{V}}}}{\pi }} \right)\left( { - \dfrac{1}{{{r^2}}}} \right) \\
   \Rightarrow \dfrac{d}{{dr}}\left( {{\text{TSA}}} \right) = 2\pi r - \left( {\pi + 2} \right)\left( {\dfrac{{2{\text{V}}}}{{\pi {r^2}}}} \right){\text{ }} \to {\text{(3)}} \\
 \]
In order to have minimum surface area of the half cylinder we will put \[\dfrac{d}{{dr}}\left( {{\text{TSA}}} \right) = 0\] in the above equation, we get
\[
   \Rightarrow 0 = 2\pi r - \left( {\pi + 2} \right)\left( {\dfrac{{2{\text{V}}}}{{\pi {r^2}}}} \right) \\
   \Rightarrow 2\pi r = \left( {\pi + 2} \right)\left( {\dfrac{{2{\text{V}}}}{{\pi {r^2}}}} \right) \\
   \Rightarrow {r^3} = \left( {\dfrac{{\pi + 2}}{{2\pi }}} \right)\left( {\dfrac{{2{\text{V}}}}{\pi }} \right) \\
   \Rightarrow {r^3} = \left( {\dfrac{{\pi + 2}}{{{\pi ^2}}}} \right){\text{V }} \to {\text{(4)}} \\
 \]
Here, if \[\dfrac{{{d^2}}}{{d{r^2}}}\left( {{\text{TSA}}} \right) \geqslant 0\] then it means that the total surface area of the given half cylinder will be minimum whereas if \[\dfrac{{{d^2}}}{{d{r^2}}}\left( {{\text{TSA}}} \right) \leqslant 0\] then it means that the total surface area of the given half cylinder will be maximum.
By differentiating equation (3) with respect to r on both sides, we get
\[
   \Rightarrow \dfrac{{{d^2}}}{{d{r^2}}}\left( {{\text{TSA}}} \right) = \dfrac{d}{{dr}}\left[ {2\pi r - \left( {\pi + 2} \right)\left( {\dfrac{{2{\text{V}}}}{{\pi {r^2}}}} \right)} \right] \\
   \Rightarrow \dfrac{{{d^2}}}{{d{r^2}}}\left( {{\text{TSA}}} \right) = \dfrac{d}{{dr}}\left( {2\pi r} \right) - \dfrac{d}{{dr}}\left[ {\left( {\pi + 2} \right)\left( {\dfrac{{2{\text{V}}}}{{\pi {r^2}}}} \right)} \right] \\
   \Rightarrow \dfrac{{{d^2}}}{{d{r^2}}}\left( {{\text{TSA}}} \right) = 2\pi \dfrac{{dr}}{{dr}} - \dfrac{{2\left( {\pi + 2} \right){\text{V}}}}{\pi }\dfrac{d}{{dr}}\left( {{r^{ - 2}}} \right) \\
   \Rightarrow \dfrac{{{d^2}}}{{d{r^2}}}\left( {{\text{TSA}}} \right) = 2\pi - \dfrac{{2\left( {\pi + 2} \right){\text{V}}}}{\pi }\left( { - 2{r^{ - 3}}} \right) \\
   \Rightarrow \dfrac{{{d^2}}}{{d{r^2}}}\left( {{\text{TSA}}} \right) = 2\pi + \dfrac{{4\left( {\pi + 2} \right){\text{V}}}}{{\pi {r^3}}} \\
 \]
By putting \[{r^3} = \left( {\dfrac{{\pi + 2}}{{{\pi ^2}}}} \right){\text{V}}\] in the above equation, we get
\[ \Rightarrow \dfrac{{{d^2}}}{{d{r^2}}}\left( {{\text{TSA}}} \right) = 2\pi + \dfrac{{4\left( {\pi + 2} \right){\text{V}}}}{{\pi \left( {\dfrac{{\pi + 2}}{{{\pi ^2}}}} \right){\text{V}}}} = 2\pi + \dfrac{4}{{\left( {\dfrac{1}{\pi }} \right)}} = 2\pi + 4\pi = 6\pi > 0\]
Clearly, from the above equation we can see that \[\dfrac{{{d^2}}}{{d{r^2}}}\left( {{\text{TSA}}} \right)\] comes out to be positive so the total surface area of the given half cylinder will be minimum.
By substituting ${\text{V}} = \dfrac{{\pi {r^2}h}}{2}$ in equation (4), we get
\[
   \Rightarrow {r^3} = \left( {\dfrac{{\pi + 2}}{{{\pi ^2}}}} \right)\left( {\dfrac{{\pi {r^2}h}}{2}} \right) = \dfrac{{\left( {\pi + 2} \right){r^2}h}}{{2\pi }} \\
   \Rightarrow \left[ {\dfrac{{2\pi }}{{\left( {\pi + 2} \right)}}} \right]\dfrac{{{r^3}}}{{{r^2}}} = h \\
   \Rightarrow h = \dfrac{{2\pi }}{{\left( {\pi + 2} \right)}}r \\
   \Rightarrow \dfrac{h}{{2r}} = \dfrac{\pi }{{\left( {\pi + 2} \right)}} \\
 \]
Since, Diameter of semi-circular ends (with radius r) = 2r and length of the half cylinder = h
 \[ \Rightarrow \dfrac{{{\text{Length of the half cylinder}}}}{{{\text{Diameter of its semi - circular ends}}}} = \dfrac{\pi }{{\left( {\pi + 2} \right)}}\]

Therefore, the ratio of the length of the cylinder to the diameter of its semi-circular ends is $\pi :\left( {\pi + 2} \right)$.

Note- The curved surface area of half cylinder having radius r and length h is equal to half the curved surface area of the cylinder having radius r and length h i.e., $\dfrac{{2\pi rh}}{2} = \pi rh$. In this particular problem, volume of the half cylinder (V) is constant because it is given that a given (fixed) quantity of metal is casted to make this half cylinder.