Question

A given object takes $n$ times as much time to slide down as ${{45}^{{}^\circ }}$ rough incline as it takes to slide down a perfectly smooth ${{45}^{{}^\circ }}$ incline. What is the coefficient of kinetic friction between the object and the incline?
$\text{A}\text{. }\left( 1-\dfrac{1}{{{n}^{2}}} \right)$
$\text{B}\text{. }\dfrac{1}{1-{{n}^{2}}}$
$\text{C}\text{. }\sqrt{\left( 1-\dfrac{1}{{{n}^{2}}} \right)}$
$\text{D}\text{. }\sqrt{\dfrac{1}{1-{{n}^{2}}}}$

Answer 1

Hint: Kinetic friction is the force that acts on two surfaces when at least one of them is moving. The magnitude of this force depends on the coefficient of kinetic friction between the two materials. The coefficient of kinetic friction is the ratio of kinetic friction force and normal reaction force on the object.

Formula used:
Net force${{F}_{net}}=ma$
Displacement due to constant acceleration $s=ut+\dfrac{1}{2}a{{t}^{2}}$

Complete step-by-step answer:
First, we assume that time taken by an object of mass $m$ to slide down on a smooth inclined plane is $t$ and a rough inclined plane is $t'$. Since the object takes $n$ times as much time to slide down rough incline as it takes to slide down a perfectly smooth incline, we have
$t'=nt$
Now we resolve the components acceleration in direction of motion and perpendicular to direction of motion.
For smooth incline, equation of motion:

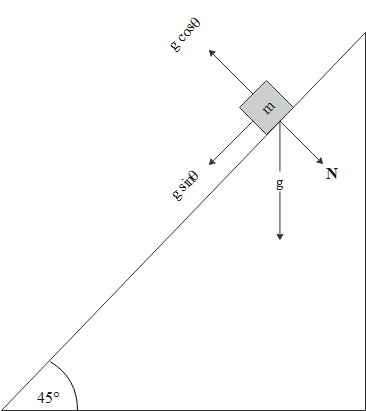
In direction perpendicular to direction of motion, the normal reaction $N$ when $\theta$ is the angle of inclination
$N=mg\cos \theta $
Along the direction of motion, net force ${{F}_{net}}$ when object accelerates with constant acceleration $a$
${{F}_{net}}=ma$
$mg\sin \theta =ma\Rightarrow a=g\sin \theta $
For rough incline, equation of motion:

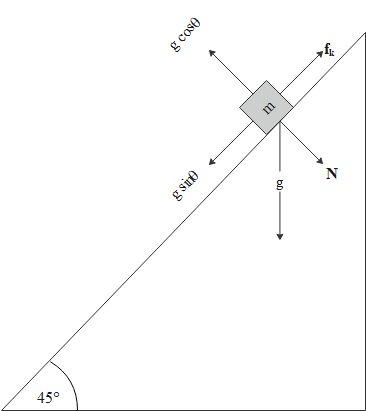
In direction perpendicular to direction of motion
$N=mg\cos \theta $
Along the direction of motion net force when object accelerates with acceleration $a'$ is
$F_{net}^{'}=ma'$
$mg\sin \theta -{{f}_{k}}=ma'$
Where kinetic friction ${{f}_{k}}=\mu N$
$\mu$ is the coefficient of kinetic friction.
$\Rightarrow {{f}_{k}}=\mu mg\cos \theta $
Therefore we get,
$a'=g(\sin \theta -\mu \cos \theta )$
Since distance travelled by object is same in both cases, we have
$s=s'$
$\left( g\sin \theta \right){{t}^{2}}=g(\sin \theta -\mu \cos \theta ){{(t')}^{2}}$
On simplifying this equation and substituting $t'=nt$ and $\theta=45^\circ$ we get
${{t}^{2}}=(1-\dfrac{\mu \cos {{45}^{{}^\circ }}}{\sin {{45}^{{}^\circ }}}){{(nt)}^{2}}$
On solving the above equation for coefficient of kinetic friction $\mu$ we get
$\mu =1-\dfrac{1}{{{n}^{2}}}$

So, the correct answer is “Option A”.

Note: Friction is a force that comes into play when two surfaces are in contact with each other when some force tries to move one body. Friction always opposes the motion of the body thus slowing it down.
Normal reaction force is the force exerted by a surface perpendicular to the surface of the object which is in contact with it.