Question

A girl standing on a lighthouse built on a cliff near the seashore, observes two boats due east of the lighthouse. The angles of depression of the two boats are \[{{30}^{\circ }}\] and \[{{60}^{\circ }}\]. The distance between the boats is 300m. Find the distance of the top of the lighthouse from the sea level. (Boats and feet of the lighthouse are in a straight line).

Answer 1

Hint: Draw the figure as mentioned. Consider h as the distance of the top of the lighthouse from sea level. The angles of depression are to be marked next. Then get the trigonometric ratios and standard angles like tangent value of \[{{30}^{\circ }}\] and \[{{60}^{\circ }}\] from the triangles formed. Solve further and find h.

Complete step-by-step answer:
Let AD be the lighthouse, where A denotes the foot of the cliff and D denotes the top of the light house.
Let B and C be the two boats. Boat B is at an elevation of \[{{60}^{\circ }}\] from the lighthouse. Similarly boat C is at an elevation of \[{{30}^{\circ }}\] from the top of the lighthouse.
Let h be the distance of the top of the light house from the sea level.

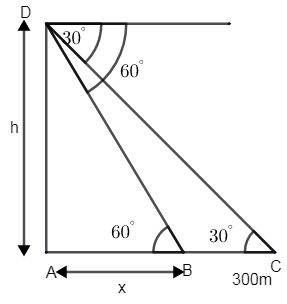
Let us consider AB = x, from the figure.
We have been given that \[\angle ABD={{60}^{\circ }}\] and \[\angle ACD={{30}^{\circ }}\].
Now let us consider \[\Delta ABD\].
\[\tan {{60}^{\circ }}\] = opposite side / adjacent side = \[\dfrac{AD}{AB}=\dfrac{h}{x}\].
From the trigonometric table we know that \[\tan {{60}^{\circ }}\] = \[\sqrt{3}\].
\[\therefore \]\[\sqrt{3}=\dfrac{h}{x}\Rightarrow x=\dfrac{h}{\sqrt{3}}\] - (1)
Now let us consider \[\Delta ACD\].
\[\tan {{30}^{\circ }}\] = opposite side / adjacent = \[\dfrac{AD}{AC}=\dfrac{AD}{AB+BC}\].
We know AB = x and BC = 300m. Put \[x=\dfrac{h}{\sqrt{3}}\].
From the trigonometric table, \[\tan {{30}^{\circ }}=\dfrac{1}{\sqrt{3}}\].
\[\tan {{30}^{\circ }}=\dfrac{AD}{AB+BC}\]
\[\dfrac{1}{\sqrt{3}}=\dfrac{h}{x+300}\], cross multiplying them we get,
\[x+300=h\sqrt{3}\], put \[x=\dfrac{h}{\sqrt{3}}\].
\[\begin{align}
  & \dfrac{h}{\sqrt{3}}+300=h\sqrt{3} \\
 & h\sqrt{3}-\dfrac{h}{\sqrt{3}}=300\Rightarrow \dfrac{3h-h}{\sqrt{3}}=300 \\
 & 2h=300\sqrt{3} \\
\end{align}\]
\[\therefore h=150\sqrt{3}\]m
Hence the height of the lighthouse from the sea level is \[150\sqrt{3}\]m.

Note: Be careful while drawing the figure, you miss a small detail or you draw wrong, then the entire answer will be wrong as it solely depends on the figure. Remember the trigonometric table values so it becomes easy to solve.