Question

A girl of height 90 cm is walking away from the base of a lamp-post at a speed at 1.2 m/sec. If the lamp is 3.6 m above the ground, find the length of her shadow after 4 seconds.

Answer 1

Hint: Here, first draw the diagram from the information given in the question to understand the given situation geometrically. Prove the triangles as similar triangles and use the property of similar triangles to find the unknown value.

Complete step by step answer:
Given, height of lamp-post = 3.6 cm, height of girl = 90 cm = 0.9 m.

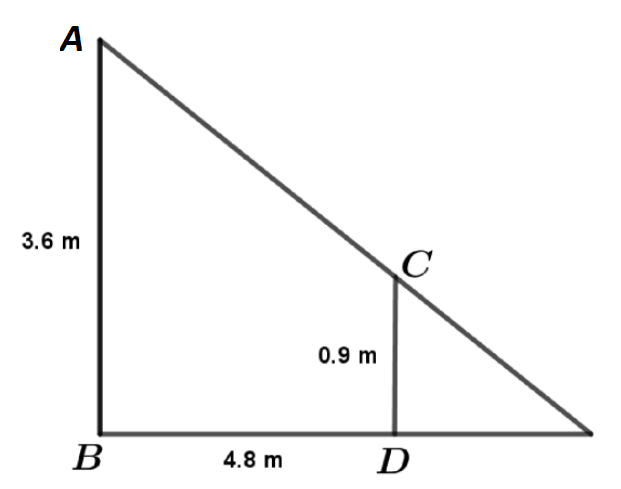
Let AB be the lamp-post of height 3.6 m, CD be the girl of height 0.9 m, DE be the girl’s shadow and BE be the shadow of the lamp-post at particular time.
Also given the girl is moving away from the post at a speed of 1.2 m/s, so distance covered in 4 seconds by the girl is $4 \times 1.2 = 4.8$m. [Since, Distance = Speed × Time]
In the figure, DE is the distance travelled by the girl in 4 seconds, therefore, DE = 4.8 m.
In triangles ABE and CDE,
$\angle ABE = \angle CDE$ [Both angles is equal to 90°]
$\angle AEB = \angle CED$ [Common in both triangles]
By AA similarity criteria,$\vartriangle ABE$ and $\vartriangle CDE$ are similar triangles.
Using property of similar triangles, $\dfrac{{AB}}{{CD}} = \dfrac{{BE}}{{DE}}$ …(i)
[If two triangles are similar, then ratio of their corresponding sides is equal]
We have, $AB = 3.6$m, $CD = 0.9$m, $BE = (4.8 + DE)$m
Putting values in equation (i), we get
$\dfrac{{3.6}}{{0.9}} = \dfrac{{(4.8 + DE)}}{{DE}}$
On simplifying the equation, we get
$4 = \dfrac{{(4.8 + DE)}}{{DE}}$
On cross-multiplying the equation, we get
$4DE = 4.8 + DE$
$ \Rightarrow 3DE = 4.8$
$ \Rightarrow DE = \dfrac{{4.8}}{3} = 1.6$
$ \Rightarrow $DE = 1.6 m

Therefore, the length of shadow of girl after 4 seconds is 1.6 m

Note:
In these types of questions always use properties of similar triangles to find the unknown values. Alternatively, in case of shadow formation at any particular, the ratio of heights of two objects is equal to the ratio of their shadows. So, you can directly compare heights and lengths of shadows.