Question

A girl of height 150cm stands in front of a lamp post and costs a shadow of length \[150\sqrt 3 \] cm on the ground. Find the angle of elevation of the top of the lamp post (in degrees).

Answer 1

Hint:Here we draw a diagram depicting the situation of a girl standing in front of a lamp post and the shadow of the girl falls on the ground. Taking the angle the girl makes with the ground as the right angle we can form a right angle triangle. We use the definition of angle of elevation to write which angle is angle of elevation in the figure and use the formula of tan of an angle to find the value of angle.

Formula used:
Complete step-by-step answer:
We are given the height of the girl is 150cm and the length of the shadow formed on the ground is \[150\sqrt 3 \]cm.
We draw a diagram depicting the situation.

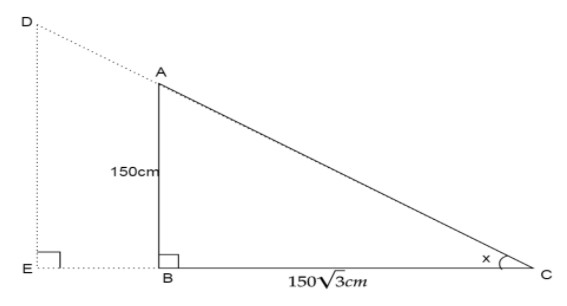
Here ED represents the lamp post, AB represents the girl and BC represents the shadow of the girl formed by the light from the lamp post.
Since, the girl stands perpendicular to the ground; we can say triangle ABC is a right angled triangle.
Then in \[\vartriangle ABC,\angle B = {90^ \circ }\]
We know from the definition of angle of elevation that it is the angle made by horizontal line with the line of sight. Here the horizontal line is the ground and the line of sight is DC. Then the angle of elevation is x.
Here the lamp post is the object and we measure the angle from the end of the shadow to the top of the lamp post.
We know tan of an angle in a right triangle is given by dividing perpendicular by base.
\[ \Rightarrow \tan x = \dfrac{{AB}}{{BC}}\]
Now we know \[AB = 150\]cm and \[BC = 150\sqrt 3 \]cm
Substitute the values in the fraction
\[ \Rightarrow \tan x = \dfrac{{150}}{{150\sqrt 3 }}\]
Cancel the same terms from numerator and denominator.
\[ \Rightarrow \tan x = \dfrac{1}{{\sqrt 3 }}\]
Now we know that \[\tan {30^ \circ } = \dfrac{1}{{\sqrt 3 }}\]
\[ \Rightarrow \tan x = \tan {30^ \circ }\]
Now since the function on both sides of the equation is equal. Then the angle has to be equal.
\[ \Rightarrow x = {30^ \circ }\]
Angle of elevation is \[{30^ \circ }\]

Note:Students might get confused between the angles of elevation here as we have to find the angle of elevation on top of the lamp post which will be the angle measured from the ground. Students might try to measure the angle from the top of the lamp post which will be \[\angle CDE\] in the diagram.