Question

A girl of height 100 cm is walking away from the base of a lamp-post at a speed of $1.9\text{ m/s}$. If the lamp is 5m above the ground, find the length of her shadow after 4 seconds.

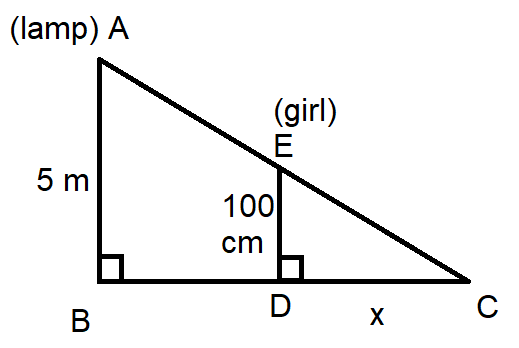
Answer 1

Hint: We first find the same angles between the $\Delta ABC$ and $\Delta EDC$. Based on the same angles we find the ratio of the similar sides. We form the relation and find the solution for the length BC which is the length of her shadow.

Complete step-by-step solution:
The lamp is AB with height being 5 m. So, $AB=5$. The representation of the girl is ED where $ED=1$ as her height is 100 cm. Her shadow is the total length of BC.
She is going at a speed of $1.9\text{ m/s}$. After 4 seconds she is at point D. So, $BD=1.9\times 4=7.6$.
We are going to use the concept of similar triangles and then use the ratio of the sides of those triangles.
In the given figure we have two triangles where we take $\Delta ABC$ and $\Delta EDC$.
It’s given that $\angle ABC=\angle EDC={{90}^{\circ }}$. Also $\angle ACB=\angle ECD$ is the common angle.
We also know that the sum of three angles of a triangle is always equal to ${{180}^{\circ }}$.
We got two angles of each triangle being equal which means the remaining angle of each triangle is also equal.
So, $\angle BAC=\angle DEC$.
We know that if three angles of two triangles are the same then the triangles are similar triangles and the ratio of opposite sides of similar angles are equal.
Therefore, for $\Delta ABC$ and $\Delta EDC$ we get $\dfrac{AC}{EC}=\dfrac{AB}{ED}=\dfrac{BC}{DC}$.
We take $\dfrac{AB}{ED}=\dfrac{BC}{DC}$ and get $\dfrac{AB}{ED}=\dfrac{BD+DC}{DC}=\dfrac{BD}{DC}+1$.
Now we put the values and get
$\begin{align}
  & \dfrac{5}{1}=\dfrac{7.6}{DC}+1 \\
 & \Rightarrow \dfrac{7.6}{DC}=5-1=4 \\
 & \Rightarrow DC=\dfrac{7.6}{4}=1.9 \\
\end{align}$
So, $BC=BD+DC=7.6+1.9=9.5$.
The length of her shadow is $9.5$ m.

Note: The concept of similar triangles and congruent triangles are two different terms that are closely related. Similar triangles are two or more triangles with the same shape, equal pair of corresponding angles and the same ratio of the corresponding sides. In Euclidean geometry, two objects are similar if they have the same shape, or one has the same shape as the mirror image of the other. More precisely, one can be obtained from the other by uniformly scaling, possibly with additional translation, rotation and reflection.